功率因数的作用及提高

随着工农业生产的迅猛发展，家用电器在城镇几乎普及。大量的异步电动机就成为电力系统的主要负载，由于异步电动机是电感性负载，在工作时除消耗有功功率外，还需要电源提供无功功率，故整个电力系统的功率因数较低。电动机满载运行时，功率因数约为0.7~0.8,轻载、空载运行时约为0.3~0.4；日光灯的功率因数也较低，约为0.4左右。功率因数低对电力系统的运行是不利的。

一是发电机的效能不能充分发挥，如发电机的额定容量为10000kVA，它能向负载提供多大的有功功率，要由负载的功率因数来决定。当负载功率因数cosφ=1时，发电机可向负载提供10000kW的有功功率，若负载功率因数cosφ=0.6,则电源提供的有功功率仅为6000kW。同样一台发电机，电路的功率因数越低，输出的有功功率越少，设备容量的利用率越低，电源的容量就不能充分利用。

另一方面，功率因数越低，输电线路上的功率损耗越大。因为线路上的电流$I=\frac{P}{Ucos\varphi }$，当电源电压U和负载的有功功率P为恒定值时，I与cosφ成反比关系，cosφ越小，I就越大，线路上的功率损耗△P=I²R₁（R₁为输电线电阻）越大，而且输电线上的电压损失也越大，使输电效率和供电质量降低。

从以上分析可知，提高负载的功率因数对电力系统有显著的经济效益，并改善了电能质量。按现行供用电规程规定，工厂配电变压器高压侧的功率因数要求在0.9及以上，如果功率因数达不到此值，就应采用无功功率补偿措施提高功率因数。

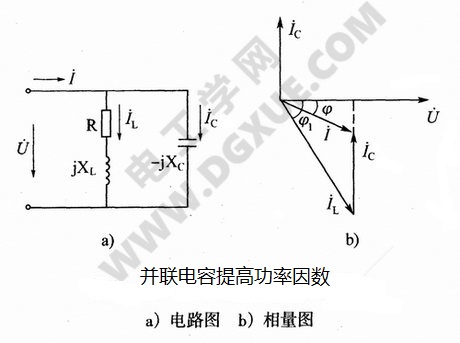
提高功率因数的常用方法是并联电容器。将电力电容器并联在电感性负载两端，或并联在变电所的高压或低压母线上，如下图所示。

并联电容器为什么能提高功率因数呢？

上图a中在并联电容前负载为电阻R和电感L串联，电路的电流为$\dot{I}_{L}$，电压为$\dot{U}$，功率因数为cosφ₁。并联电容C后，电容支路电流为$\dot{I}_{C}$，此时电路总电流$\dot{I}=\dot{I}_{L}+\dot{I}_{C}$。由相量图可知，由于电路中增加了一个超前电压$\dot{U}90°$的$\dot{I}_{C}$，则$\dot{I}$滞后$\dot{U}$的角度减小为φ，显然φ＜φ₁，也就是cosφ＞cosφ₁。而且总电流的有效值也减小了，输电线路的电压损失、功率损失也减小。并联电容后感性负载本身的电压、电流、功率都是不变的。

将功率因数由cosφ₁提高到cosφ要并联多大的电容呢？由图b可知，在保持负载有功功率不变的条件下，将cosφ₁提高到cosφ，此时的电容电流${I}_{C}$为：

$$ \begin{align}
I_{C} & =\left ( I_{L}cos\varphi _{1} \right )tan\varphi _{1}-\left ( Icos\varphi \right )tan\varphi \\ & =\frac{P}{U}\left ( tan\varphi _{1}-tan\varphi \right )\end{align}$$

将$I_{C}=\frac{U}{X_{C}}=U2\pi fC$代入上式，整理后得：

$$C=\frac{P}{2\pi fU^{2}}(tan\varphi _{1}-tan\varphi )$$

补偿电容的无功功率为：

$$Q_{C}=UI_{C}=P(tan\varphi -tan\varphi )$$

在上边的式子中:

• P是电源向负载供给的有功功率（W）；
• $f$为电压的频率（Hz）;
• U为负载的额定电压（V）；
• cosφ1为并联电容前感性负载的功率因数；
• cosφ为并联电容后的功率因数；
• C为补偿的电容值（F）；
• Q_C为补偿电容器产生的无功功率（var）。