瞬时功率、有功功率、无功功率、视在功率讲解

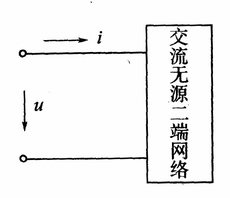由电阻、电感和电容组合而成的电路在工作时要从电源吸取功率，显然此功率与单一参数电路的功率是不完全相同的。本篇将三种元件组合成的电路作为一个无源二端网络讨论其功率，不涉及电路内部的组合方式，如右图所示。

设流入该二端网络的电流$i=I\sqrt{2}sin\omega t$，二端网络两端点之间的电压$u=U\sqrt{2}sin\left ( \omega t+\varphi  \right )$，二端网络的等效复阻抗$Z=|Z|\angle \varphi $。

瞬时功率

二端网络在某瞬时吸收的功率称为瞬时功率，用符号p表示。

$$ \begin{align} p & =ui\\ & =U\sqrt{2}sin\left ( \omega t+\varphi  \right )\times I\sqrt{2}sin\omega t
\\ & =UI\left [ cos\varphi -cos\left ( 2\omega t+\varphi  \right ) \right ]\end{align}$$

从上式中可知，瞬时功率总是随时间而变化的，当p为正值时，表示二端网络从电源吸收功率；当p为负值时，表示二端网络向电源释放功率。

有功功率

由于瞬时功率随时间不断地变化，工程上应用很不方便。在工程上常用的交流电路的功率是指有功功率，即取瞬时功率在一个周期内的平均值，又称为平均功率，并用P表示，有功功率的单位是W或kW。

$$ \begin{align} P &  =\frac{1}{T}\int_{T}^{0}pdt\\  & =\frac{1}{T}\int_{T}^{0}UI\left [ cos\varphi -cos\left ( 2\omega t+\varphi  \right ) \right ]dt\\ &  =UIcos\varphi\end{align}$$

从上式可知，有功功率是一个不随时间变化的恒定值。因为二端网络中有电阻、电感和电容，而电感、电容是不消耗有功功率的，所以有功功率就是二端网络中电阻所消耗的功率。如日光灯的额定功率是40 W，就是指日光灯等效电路中电阻所消耗的功率是40 W。

上式表明有功功率不仅与电压、电流有效值的乘积有关，还和电压与电流相位差角φ的余弦函数有关。式中的cosφ为电路的功率因数，φ角也称为功率因数角。由于φ角是二端网络复阻抗的阻抗角，所以功率因数是由二端网络的参数和频率决定的。

无功功率

在二端网络中，由于有电感、电容，它们虽然不消耗电能，但与电源之间有能量的交换。从前述单一参数交流电路中可知，对电感，有$Q_{L}=U_{L}I$；对电容，有$Q_{C}=U_{C}I$。故二端网络总的无功功率是全部电感和电容无功功率的代数和。应该注意到，在同一交流电流作用下，或在同一交流电压作用下，无论是并联还是串联电路，电感和电容瞬时功率的符号始终是相反的。在串联电路中电流$\dot{I}$是同一电流，但电压$\dot{U}_{L}$和$\dot{U}_{C}$反相；并联电路中电压$\dot{U}$是同一电压，但电流$\dot{I}_{L}$和$\dot{I}_{C}$反相。所以，电路无功功率代数和为：

$$Q=Q_{L}-Q_{C}=UIsin\varphi $$

由前文《R、L、C串联和并联的正弦稳态电路》中的阻抗三角形图可知：

$$\begin{matrix}
cos\varphi =\frac{R}{|Z|}\\
sin\varphi  =\frac{X}{|Z|}
\end{matrix}$$

由此可得有功功率和无功功率分别为：

$$\left.\begin{matrix}
P=UIcos\varphi =UI\frac{R}{|Z|}=I^{2}R\\ \\
Q=UIsin\varphi =UI\frac{X}{|Z|}=I^{2}X\\
\end{matrix}\right\}$$

视在功率

二端网络的总电压和总电流有效值的乘积称为视在功率，用符号S表示，即：$S=UI$，视在功率的单位是伏安（VA），或千伏安（kVA）。

在工程上，常用视在功率来表示电气设备的额定容量，如变压器。电气设备的额定视在功率等于额定电压和额定电流的乘积，即$S_{N}=U_{N}I_{N}$。例如，一台视在功率为10000kVA的发电机，当负载功率因数$cos\varphi =1$时，能发出1000kW的有功功率，当负载功率因数$cos\varphi =0.6$，电压、电流达到额定值时，它仅能发出6000kW的有功功率。

有功功率P，无功功率Q和视在功率S三者之间的关系为：

$$\begin{matrix}
P=Scos\varphi \\
Q=Ssin\varphi \\
S=\sqrt{P^{2}+Q^{2}}\\
\varphi =arctan\frac{Q}{P}
\end{matrix}$$

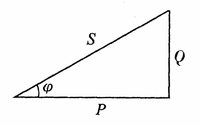
且三者也可以组成一个直角三角形，如图所示，此三角形叫做功率三角形。

若二端网络中含有多个不同功率因数的负载时，每个负载的视在功率分别以S₁、S₂、S₃……表示，但总的视在功率：

$$S\neq S_{1}+S_{2}+S_{3}+\cdots $$

在求总视在功率时，应分别求出总有功功率P和总无功功率Q，然后根据功率三角形再求出视在功率。即：

$$\begin{matrix}
P=P_{1}+P_{2}+P_{3}+\cdots\\
Q=Q_{1}+Q_{2}+Q_{3}+\cdots\\
S=\sqrt{P^{2}+Q^{2}}
\end{matrix}$$