正弦交流电正弦量三要素：频率、幅值、初相位

周期、频率与角频率

周期是正弦量变化一周所需要的时间，用符号T表示，单位是秒（s）。频率则是每秒钟内正弦量变化的次数，用符号f表示，单位是赫兹（Hz）。显然，周期与频率之间互为倒数，即：

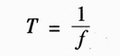
我国电力系统采用的标准频率（简称工频）是50Hz，周期为0.02s，而美国、日本等国电力标准频率为60Hz。在其他技术领域内还使用着不同频率的交流电，如中频感应炉的频率是500~ 8000Hz，无线电通讯的频率高达几十万至几亿赫兹。

正弦量变化的快慢，用每秒变化多少次（频率f）来表示，而每变化一次，对正弦函数而言，正好变了360°电角度，或2π弧度，因而用每秒变化多少弧度（称为角频率ω）也是表示正弦量变化快慢的方法，显然：

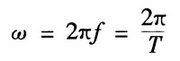
工频交流电的角频率ω=2π×50=314rad/s（弧度/秒 ）。

幅值与有效值

正弦量随时间变化过程中出现的最大数值称为幅值，也叫最大值，即为式前文中介绍的Im和Um。对于一个给定的正弦量，其幅值是恒定不变的，是表示正弦量的一个要素。然而，幅值只是特定瞬时出现的数值，它不能用来反映正弦量做功的效果，为此，引入了“有效值”的概念，用有效值来衡量交流电做功的能力。正弦交流电流、电压的有效值分别用符号U和I来表示。

正弦电流的有效值是根据电流的热效应来确定的。规定如果正弦电流i通过电阻R时，在一个周期内电阻R所消耗的电能与某直流电流I通过同一电阻R在同样长的时间内所消耗的电能相同，则该直流电流I的数值就是正弦电流i的有效值，如图下图所示。

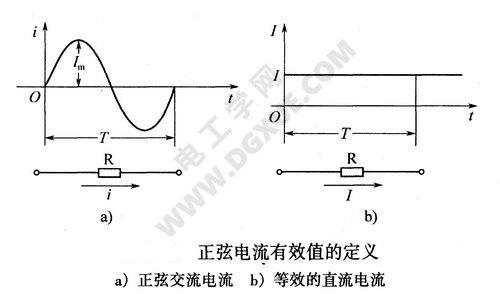
正弦电流的有效值I计算方法如下：

正弦电流在一个周期T内，电阻上所消耗的电能为：

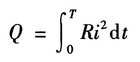
在相同时间内，直流电流在电阻上所消耗的电能：

令两式相等，即：

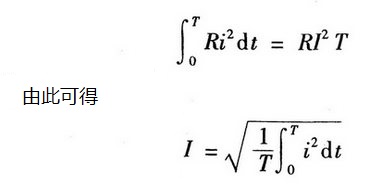
因此，有效值又叫做均方根值或方均根值。将正弦电流i=I_msin（ωt+ψ_i）带入上式中得：

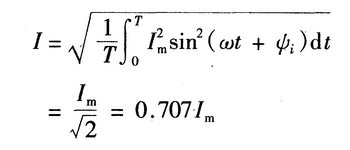
同理，对于正弦电压、电动势分别有：

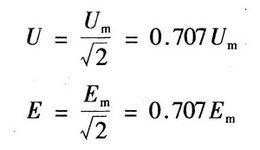
通常工农业生产所用的照明电压为220V，就是正弦电压的有效值。其最大值为220√2=311V。电气设备额定值中所标明的额定电压和电流均是指有效值。测量所用的交流电流表和电压表也是按有效值来刻度的。说明某电气设备或元件的耐压要求有时会用最大值标注。

相位、初相位和相位差

在正弦电流的函数表达式i=I_msin（ωt+ψ_i）中，（ωt+ψ_i）决定了正弦电流所处的状态，即决定了正弦电流随时间交变过程中瞬时值的数值和正负，（ωt+ψ_i）称为正弦电流的相位。相位是用角度来表示的，又称为相位角，单位为弧度（rad）或角度（°）。

时间t=0时的相位称为初相位，简称初相，正弦电流的初相位用符号ψ_i表示，单位与相位相同。它反映了正弦电流的初始值，若ψ_i=0°，则t=0时，电流的初始值为零。当ψ_i≠0°，在t=0时，电流的初始值就不为零。即：

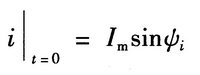
同理，正弦电动势、正弦电压的初相位可以用符号ψ_e、ψ_u来表示。

相位差就是两个同频率正弦量的相位之差，用符号φ表示，单位与相位相同，不同频率的两个正弦量，则无相位差可言。

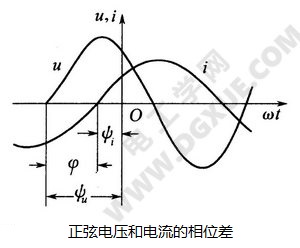
上图所示的u和i的波形用三角函数式表示为 ：

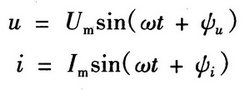
它们的相位之差为：

上式说明，两个同频率正弦量的相位差等于它们的初相位之差，是一个不随时间变化的恒定量。当φ为正值时，称前者超前于后者，或称后者滞后于前者。如在图中，电压u超前电流的角度为φ，也可说电流滞后于电压φ角。φ为负值时，则称前者滞后于后者。

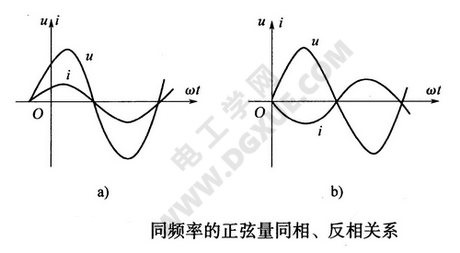
若两个同频率正弦量的相位差等于零，则称它们为同相，如下图a所示，u和i是同相关系，即它们同时达到零值、正最大值和负最大值。若两者的相位差为180°，则称为反相，如图b所示，u和i是反相关系。

频率、幅值、初相位是构成正弦量的主要特征因素，统称为正弦量的三要素。只要三要素确定了，正弦量的波形图和三角函数式就完全可以确定下来。