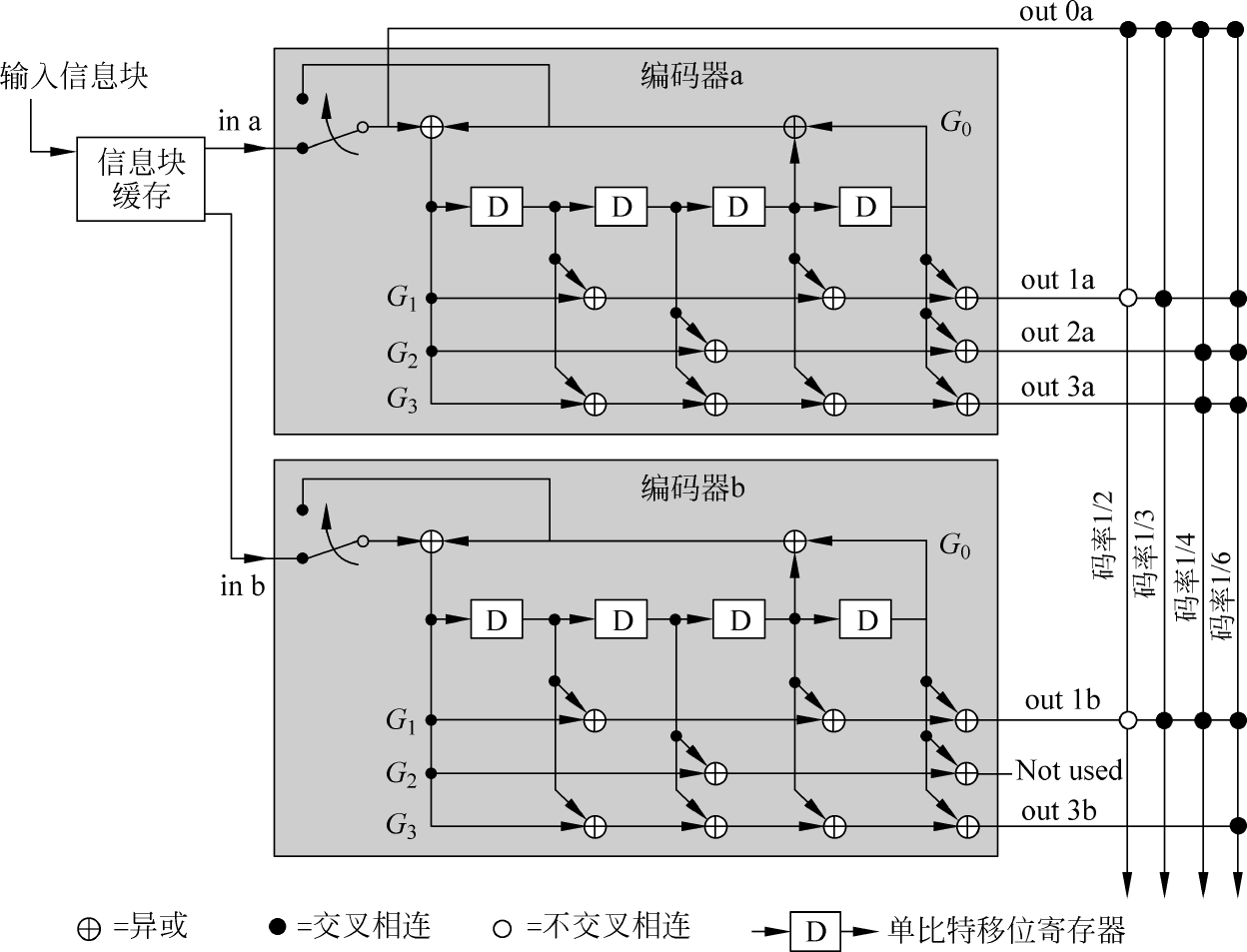
基本原理

测速是指对探测器与地面测控站天线之间的径向相对运动速度进行测量，如图1-6所示，设目标距离为R₀、目标速度v_A、测控站B与探测器A方向矢量AB，矢量夹角为α，则探测器相对于测控站之间的径向相对速度为v_A在AB方向上的分量v_AB=v_Acosα。

测速的基本原理是基于无线电信号在空间传播时的多普勒效应。当目标向测控站接近时，测控站收到的无线电信号波长变短、频率变高；当目标远离测控站时，无线电信号波长变长、频率变低。这种现象就称为“多普勒效应”。定义目标接近测控站时的速度为负，远离测控站时的速度为正。多普勒频率为接收信号频率减去发射信号频率，即f_d=f_R-f_T，其中f_d为多普勒频率（Hz），f_R为测控站接收信号频率（Hz），f_T为目标发射信号频率（Hz）。

设在t时刻，目标A发射信号的频率和初始相位分别为f_T和θ，目标距离测控站R（t）=R₀，则该时刻的发射信号相位为

假设目标相对测控站以匀速v_AB运动，经过t′时间后，目标距离测控站距离为R₀+v_ABt′，t+t′发射信号瞬时相位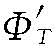为

t时刻发射信号相位到达接收机的时刻为

t+t′时刻发射信号相位到达接收机的时刻为

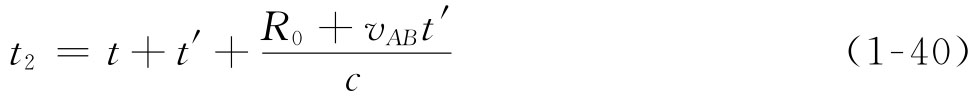
所以，在t₂-t₁=t′+v_ABt′/c时间内，测控站接收信号相位变化了2πf_Tt′，由此可得测控站接收信号频率为

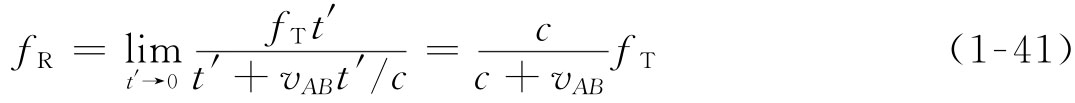
多普勒频率为

已知多普勒频率，可进一步计算目标的径向速度：

测速模式

如图1-7所示，深空探测器的无线电测速一般分为单向测速、双向测速和三向测速三种模式。

单向测速

探测器信标机发射标称频率的信标信号，地面测控站完成信标信号的接收和频率测量，利用测量频率减去标称发射频率即得到单程多普勒频率，进而可以得到飞行器的径向速度，如图1-8所示。可见，单向测速为非相干测速。

单向测速由于只需要接收测控站和探测器信标机，所以地面设备和星上设备简单。单向测速的精度主要取决于信标机频率标准的准确度和稳定度。设信标机下行频率偏移为Δf，由于多普勒测量频差Δf而引入的测速误差为Δv_AB=

对一颗行星进行探测时，可能存在多个探测器同时存在的情况，包括在轨航天器、着陆器、巡视器等。采用单向测速、VLBI测角以及遥测数据接收，可以同时对多个航天器进行测控支持，而不需要多路上行信号。这种配置可以更有效地利用测控站资源，并能够利用差分测量提高轨道测量和着陆器的位置测量精度。但受限于信标机频率标准的性能，单向测速模式的测速精度较差。

双向测速

双向测速是指测控站发射上行信号，探测器应答机接收上行信号并根据相干转发比完成下行载波的相干转发；测控站通过测量返回信号的多普勒频率计算探测器相对于测控站的径向飞行速度，如图1-7（b）所示。

深空测控站一般都配有高稳定度的原子频率标准，所有频率信号都依据该频率标准产生。由于探测器应答机完成上行信号频率的相干转发，所以探测器和地面测控站上、下行载波频率的准确度都决定于地面测控站的原子频率标准。

图1-9为双向测速系统原理框图。双向测速适用于测控弧段内单测控站能够完成信号收发的情况，是深空测速过程中使用最多、精度最高的测速手段。

相干转发比定义为探测器应答机处于相干载波转发状态时，发射的下行载波频率和接收的上行载波频率之比，表1-4给出了S、X频段上行和下行信号深空探测器的转发比。

设地面站在t-R₀/c时刻发送的信号频率为f_gt（t-R₀/c），探测器相对于测控站的速度为v_AB（t），则应答机在t时刻接收到信号的频率为

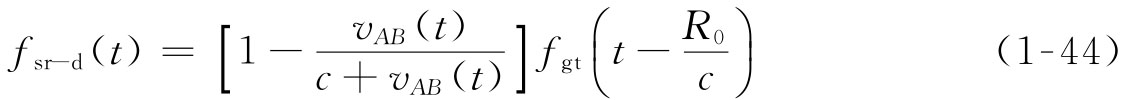
设应答机的相干转发比为ρ，则应答机在t时刻发射信号频率为

在t+R₀/c时刻测控站接收到应答机返回的信号，信号频率可以表示为

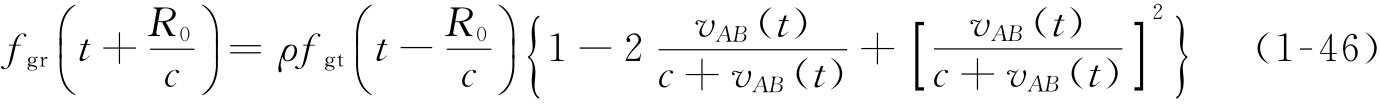
因为v_AB（t）≪c，所以忽略项，根据测控站在t-R₀/c时刻发射信号的频率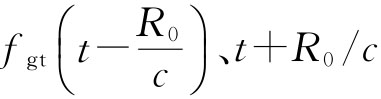时刻测量得到的接收信号频率，可以计算得到t时刻探测器相对于测控站的运动速度v_AB（t）：

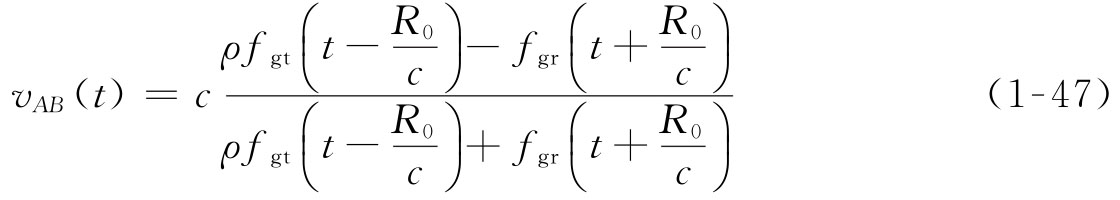
嫦娥一号探月采用S频段，设下行信号标称频率为2.25GHz，表1-5为其各阶段的最大速度、最大加速度，以及最大多普勒频率和多普勒频率变化率。

三向测速

随着深空探测器与地球之间距离的逐渐增大，受地球自转影响，发射上行信号的测控站可能无法接收到探测器相干转发的下行信号，因此需要使用另一个测控站完成下行信号的接收。或者，由于其他原因需要采用不同的测控站分别完成上行信号的发射和下行信号的接收。

如图1-7（c）所示，三向测速由一个地面测控站完成上行信号的发射，发射信号经目标应答机相干转发后由另一个地面测控站完成返回信号的接收。三向测速的物理含义是某一时刻探测器相对于发射站的径向速度与接收站的径向速度之代数和。

图1-10为三向测速系统构成原理简图。应答机部分和双向测速系统是完全相同的。2个地面测控站均配有高精度的原子钟频标设备，2个测控站之间的时间系统也是独立的。2个测控站之间的频率标准和时间标准之间的差异，导致了一定误差的产生。三向测速系统的测速精度优于单向测速，但较双向测速差。

设地面测控站A在t-R₀/c时刻发送上行信号频率为f_gt（t-R₀/c），探测器相对于测控站B的运动速度为v_AB（t），则探测器在t时刻接收信号的频率为

设应答机相干转发比为ρ，则应答机在t时刻转发信号的频率为

设在t时刻探测器与测控站C之间的距离为R₁，探测器相对于测控站C的运动速度为v_AC（t），则测控站C接收信号频率为

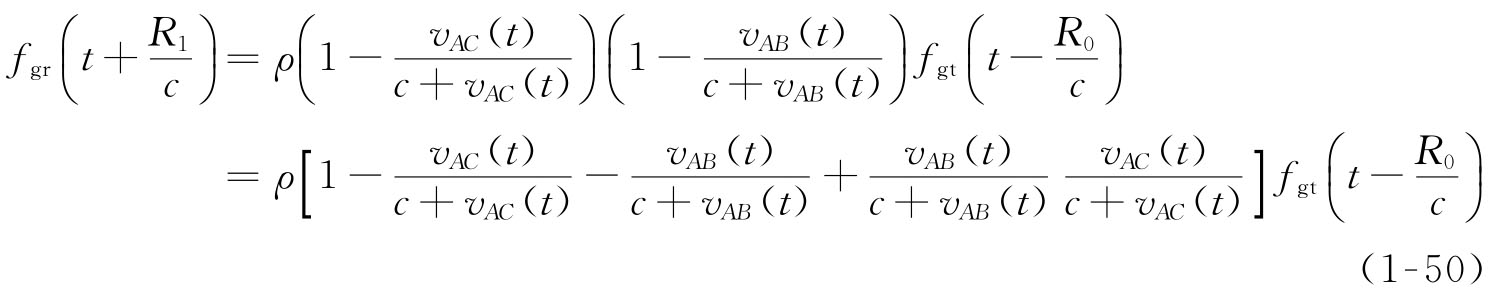
上式第二项是由于探测器相对于接收站C运动造成的多普勒频率，第三项是由于探测器相对于发射站B运动造成的多普勒频率，第四项为上行信号受接收站C相对于探测器运动造成的多普勒频率。由于v_AB（t）≪c，v_AC（t）≪c，式（1-50）可以简化为：

由此，根据发射站B在t-R₀/c时刻的上行信号频率f_gt（t-R₀/c）、接收C站测量得到的t+R₁/c时刻下行信号频率，可以计算得到t时刻探测器相对于2个测控站方向上的速度之和：