频率估计方法主要分为两大类：一类是频率搜索方法，例如比相法、离散傅里叶变换法，这类方法不考虑信号的模型，而在所需的频谱范围内进行大范围并行搜索，这种方法简单、易于实现，但是精度较低；另一类方法是基于参数化的估计方法，即先对信号进行参数化建模，然后根据接收样本对模型参数进行估计，如AR模型法，参数化测频法精度较高，但对初始误差较敏感，并且捕获范围较小，计算量较大。

在深空通信中，往往得到的频率预报有限，需要在大范围内完成频率捕获，并且要求在一定时间内完成，因此，在频率粗捕获阶段一般采用非参数的频率估计方法。

最优估计算法：残留载波体制载波频率估计模型可以假设为白噪声背景下单频信号频率估计。研究在单载波信号形式、白噪声干扰特性下最优的捕获算法，在参数估计中，由于观测噪声及其他因素的存在，会导致估计参数与真实参数存在误差；在实际估计过程中，往往要求估计是无偏的。根据分析，基于周期图的估计算法，其估计结果是无偏的，即

由于噪声的影响，单次估计结果存在偏差，代表最佳估计性能的是克拉美罗下界

根据指标要求，捕获的是单载波加白噪声的情况，一个直接简单而有效的单点频率估计方法是标准周期图估计法。

周期图应用的一大优点是运算简单，并且，如果运算频率f以f_k=k/N（k=0，1，…，N-1）采样，N次周期图运算可以被高效的FFT算法实现。采用FFT估计的过程是寻找周期图输出的最大值或周期图输出超过某一确定门限作为频率估计。门限法判别效率高，在大范围频率捕获过程中得到广泛应用。然而，由于输入噪声的影响，周期图输出是随机的，其随机性会导致虚警和漏判。

不考虑栅栏效应，并假设估计频率分辨率与观测时间呈倒数关系。对于频率f₀的周期图输入可作以下假设

式中　n=0，1，…，N-1；

q（n）——零均值高斯随机序列。

H₁假设为接收信号中含有频率f₀，接收信号中只含有噪声或者正弦信号但频率不是f₀的情况为H₀假设。于是门限法周期图估计分为3步：首先进行FFT，然后寻找峰值，最后将该值与门限比较。如果超过门限，则认为信号在该估计频段有信号并完成频率估计。显然，频率估计的虚警概率和检测概率与门限相关。为了得到精确分析，首先分析周期图输出的概率分布。

FFT其余频点概率分布一致，任何一个频点的周期图结果大于设定门限就会引起虚警，经计算虚警概率为

式中　v_T——周期图门限；

f_q（u）——噪声信号周期图计算结果概率分布函数，；

δ²——零均值高斯随机序列方差。

检测概率为

式中　f_s（u）——含噪声的有用信号的周期图计算结果概率分布函数。

单正弦波信号的最大似然估计可以通过寻找周期图峰值实现，并且该方法可以达到克拉美罗下界，因此，在高信噪比情况下，FFT峰值搜索法误判概率很低。这时如果不考虑栅栏效应，所得到的频率估计方差可以达到克拉美罗下界。

然而，FFT峰值搜索法是一个非线性的运算，在低信噪比的情况下，其他频点的周期图输出超过f₀概率增加，这时我们称之为发生了误判。在单正弦波情况下，由前面的分析可以看到：除了频点f₀外，其余FFT频点同分布，因此，误判条件下的频率估计输出在FFT频段内均匀分布，导致频率估计方差急剧恶化。FFT最大值判决发生误判的概率为

由于每点的分布是相互统计独立的，因此误判概率可以表示为

如前面分析：没有误判的情况下，得到的频率估计均方误差为克拉美罗下界值；在有误判的条件下，均方误差（MSE）由均匀分布的频率估计引起。即

式中　C——误判引起的均方误差，为常量。

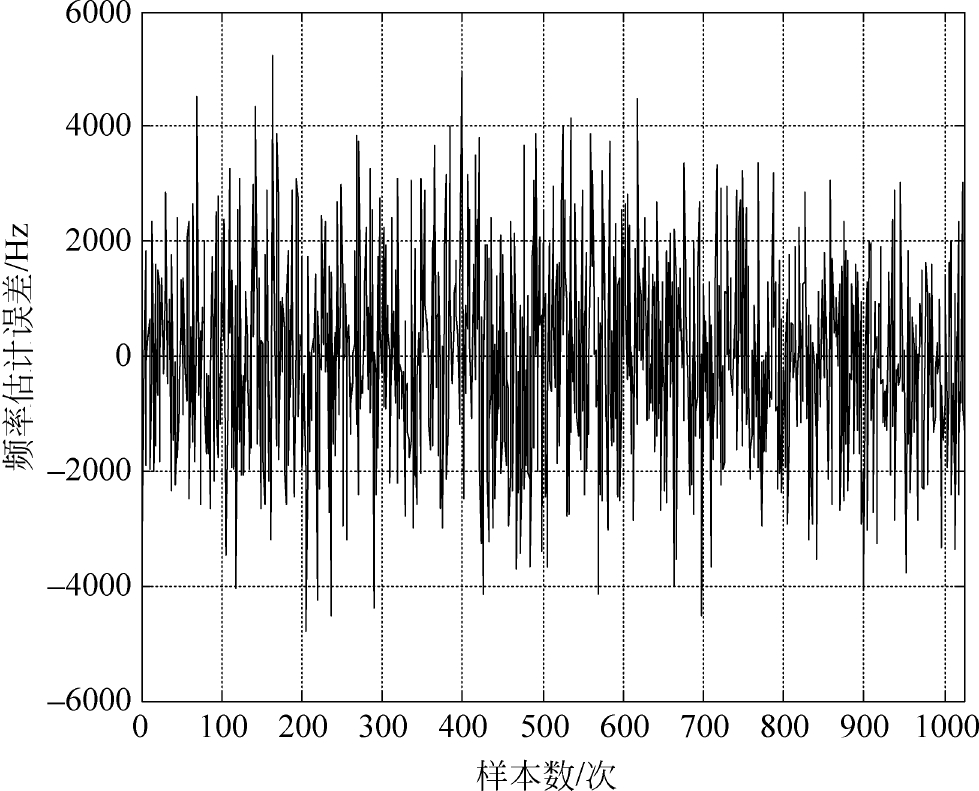
图5-48表示256点实数FFT算法下频率估计均方误差与输入信噪比的关系，其中，实曲线表示无栅栏效应下FFT估计的理论MSE。可以看出：当信噪比高于-5dB时，256点FFT估计性能接近克拉美罗下界；当输入信噪比低于-5dB时，估计性能急剧恶化，出现门限效应。

图5-48　最优算法仿真结果