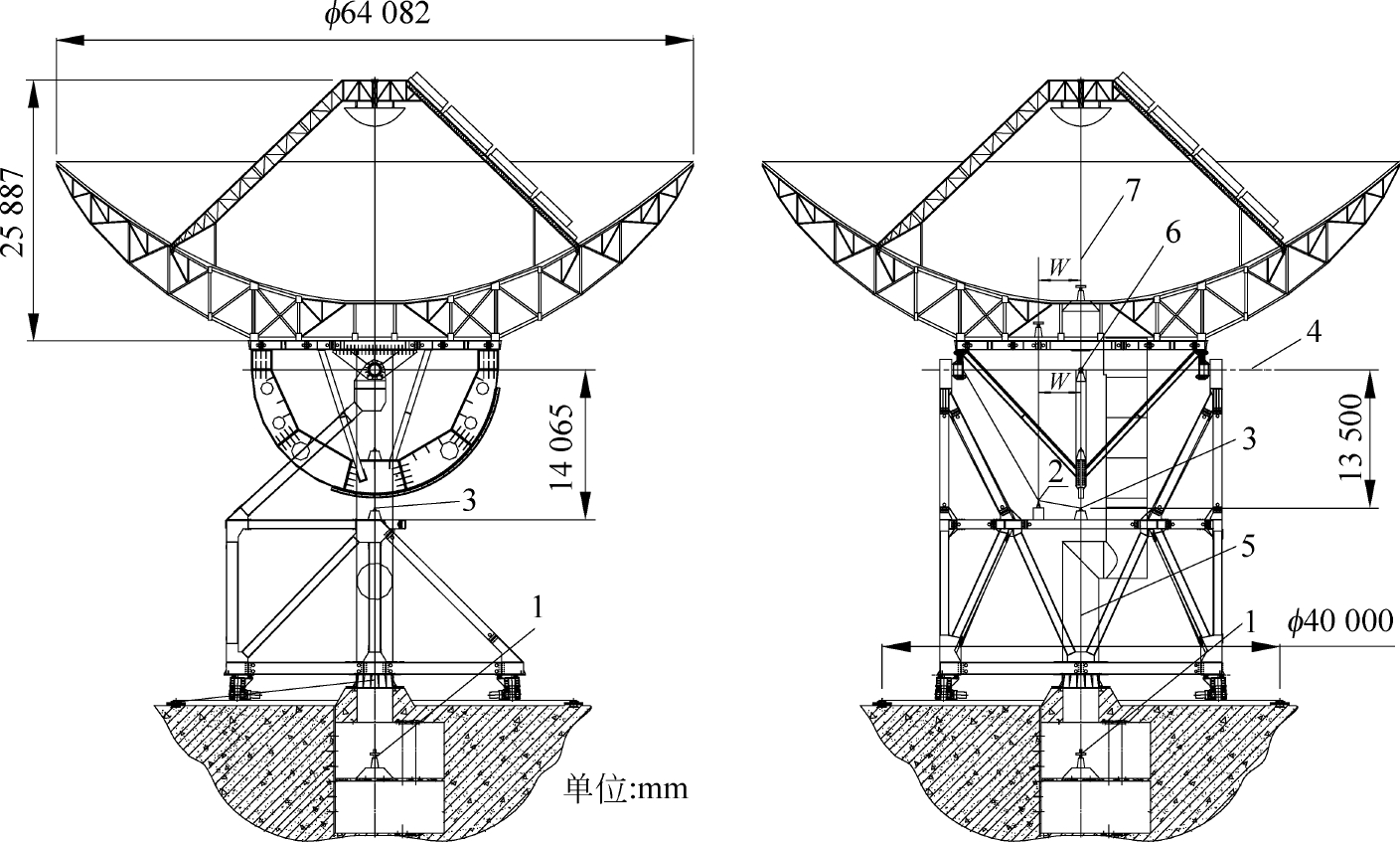
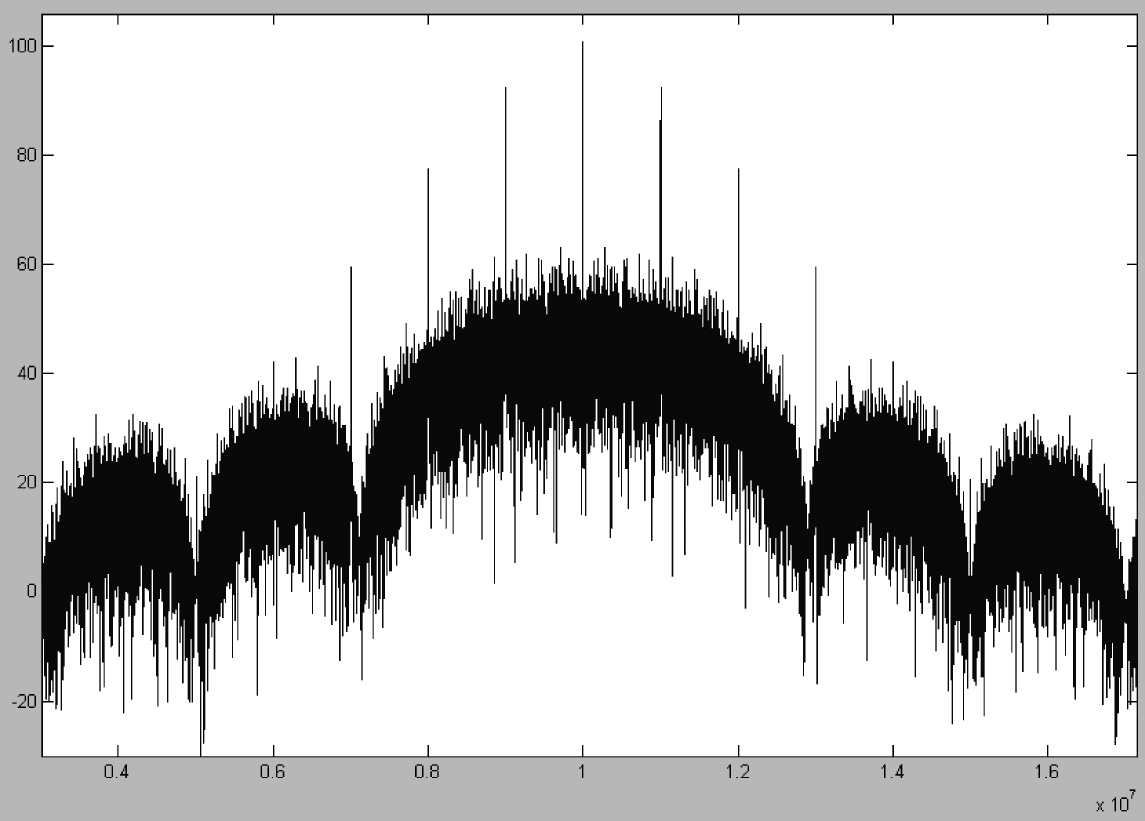
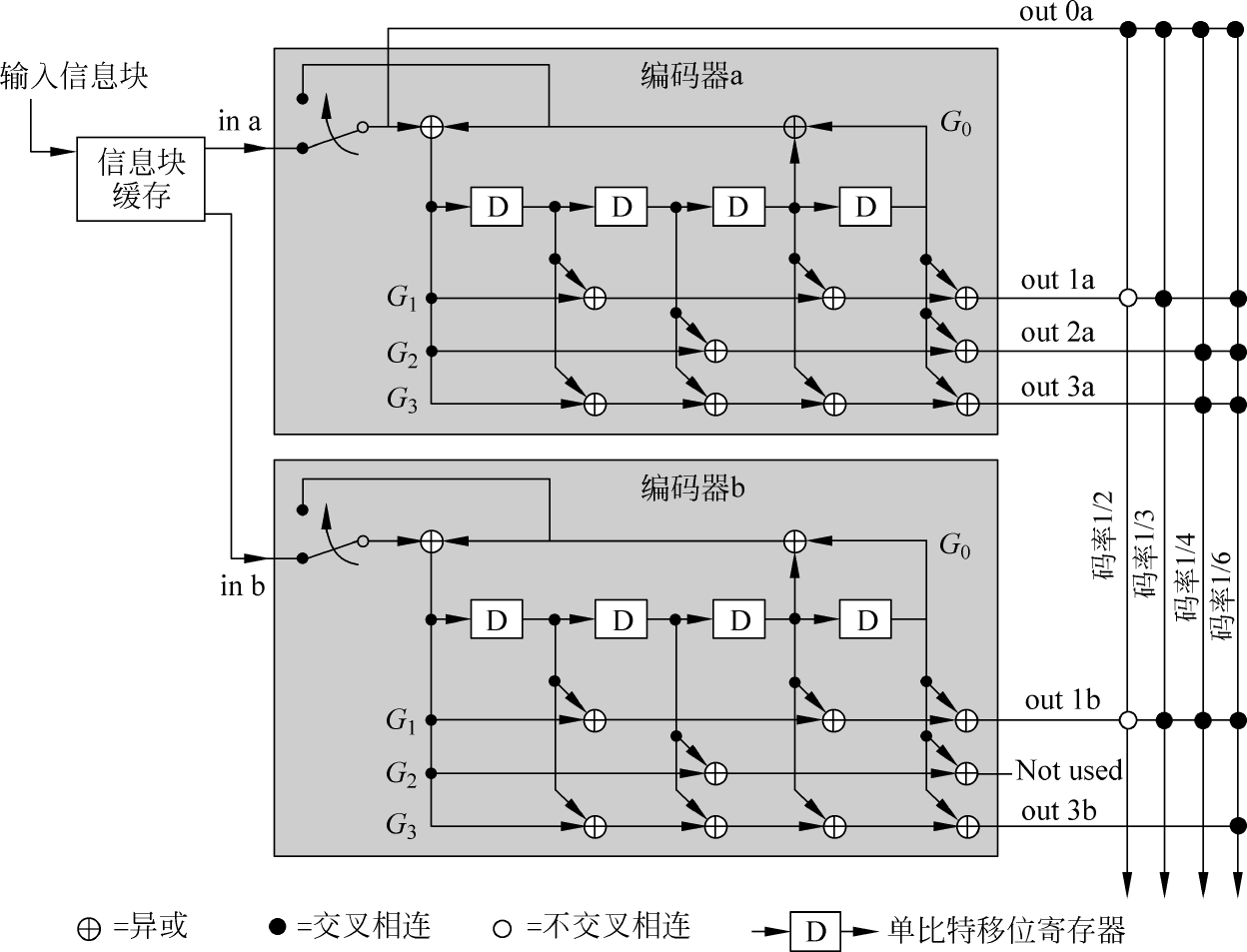
波束波导系统是整个天线系统的关键部分,由屏蔽筒、反射镜(平面镜、曲面镜)、六自由度调整机构组成。电磁波通过反射镜的多次反射才能到达馈源,实现电磁波的接收与发射,可见反射镜的位姿对天线系统的射频性能起到关键作用。因此怎样调整反射镜,使得每一个反射镜的实际位姿和理论位姿相比较在允许范围之内,是一个技术难点。
调整方案
反射镜调整就是将反射镜调整到理论位置。如果能够检测出反射镜的理论位置在哪里,反射镜实际位置在哪里,就可以知道应该将反射镜向哪个方向调、该调多少。
激光跟踪仪的功能是能够测出靶标的坐标位置并且能够跟踪靶标的运动轨迹,画出轨迹曲线。应用这个功能就可以测出反射镜的理论位置和实际位置,但必须先解决以下问题:
如何进行坐标转换
激光跟踪仪以仪器中心作为坐标原点,垂直向上的方向作为Z轴方向,水平任意方向作为X轴方向,每次仪器改变位置都会建立新的坐标系,所以仪器改变位置后必须进行坐标转换,和原来的坐标系建立关系,才能够将坐标系统一。根据三点定位的原理,只要测出同样3个点分别在2个坐标系中的位置坐标,就可以确定这2个坐标系的关系,进行坐标转换。
如何检测出方位/俯仰轴
因为激光跟踪仪能够跟踪靶标的运动轨迹,画出轨迹曲线,所以只要将靶标固定在随方位/俯仰转动的地方,然后转动方位/俯仰轴,激光跟踪仪就可以画出一段圆弧。圆弧中心垂直于圆弧平面的轴线即为方位/俯仰轴。
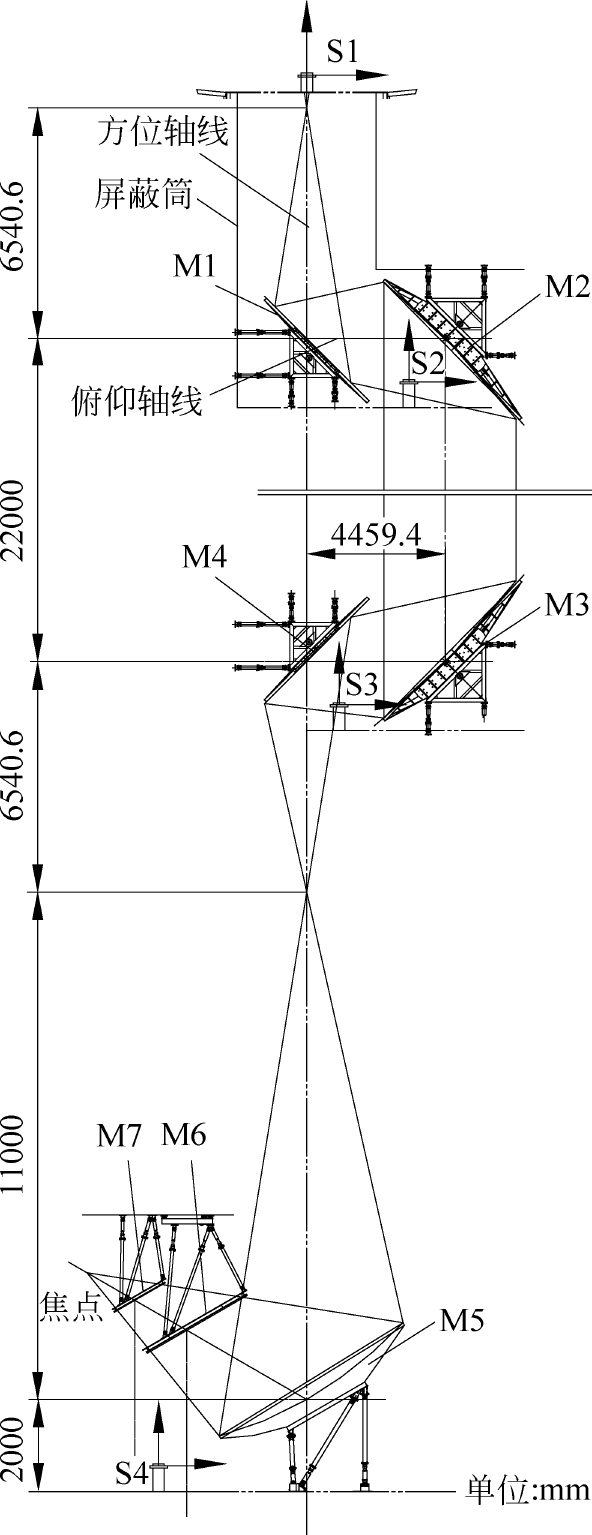
图2-39 波束波导反射镜系统图
如何确定反射镜的位置和姿态
在反射镜上设置了5个检测点,用激光跟踪仪测出这5个点的坐标值,然后和这5个点的理论位置进行比较,就可以得出反射镜的位置和姿态的偏差值。
图2-39是DSF1波束波导反射镜的理论位置图,图中的S1、S2、S3、S4是激光跟踪仪的4个坐标位置。
检测、调整步骤如下:
- 将激光跟踪仪架设在S1处,将靶标设在天线以外的脚手架上,转动天线方位,得到方位轴;
- 然后用前述的坐标变换方法将激光跟踪仪移到S2处,将靶标放在随俯仰转动的屏蔽筒内壁上,转动天线俯仰,得到俯仰轴;
- 在S2处可以测出M1、M2的位置和姿态,用仪器监视,将M1、M2反射镜调整到位;
- 将激光跟踪仪移到S3处,可以将M3、M4反射镜调整到位;
- 将激光跟踪仪移到S4处,可以将M5、M6、M7反射镜调整到位。
反射镜调整机构
DSF1的反射镜调整机构有两种形式,M1、M2、M3、M4为平行杆系结构,M5、M6、M7为交叉杆系结构,如图2-40和图2-41所示。平行杆系的调整机构在X、Y、Z三个方向上的调整比较直观。交叉杆系结构是基于Stewart运动平台设计的,该结构形式刚度较好,结构稳定,具有较高的承载能力;各个关节累积的误差相对较小,输出精度高,但是该结构控制算法较复杂。无论是平行杆系结构还是交叉杆系结构,都可以看作是一种并联机构。并联机构定义为动平台、静平台以及连接二者的多条开式运动支链组成的多闭环机械结构。对每个反射镜机构而言,其反射镜可以看作是动平台,固定支座可看作静平台,而支撑反射镜的多个杆件组成并联运动支链。每一条支链由双头螺杆组成,通过两端的虎克铰链分别与动、静平台相联。2个螺杆分别为左旋和右旋,通过螺旋副来改变各支链的长度,从而使动平台反射镜的位姿发生变化。
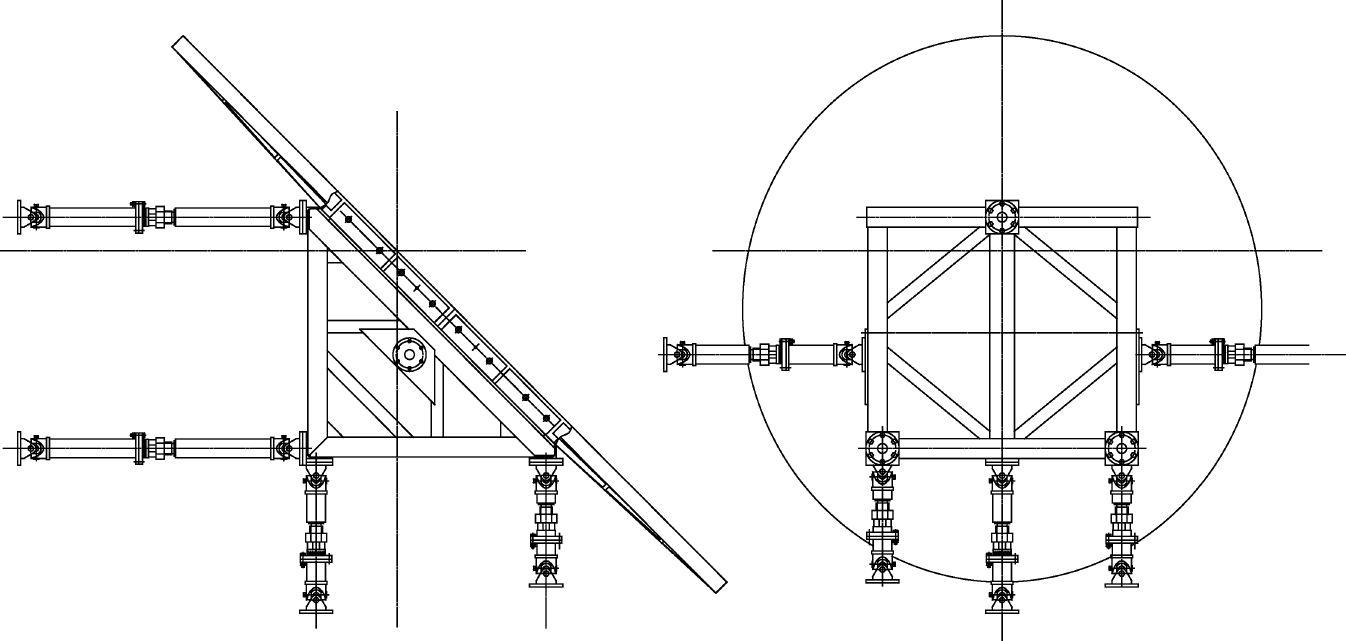
图2-40 平行杆系调整机构结构图
因此,假如已知动平台的位移和转角,求出每根支链的长度,就可以对反射镜的位姿进行调整,这是一个求并联机构逆解的过程。怎样有效、准确地求出并联机构的逆解是镜面位置调整的核心问题。为此开发了一套软件程序,能够直观、快速地计算出每根支链所需的调整量。现场调整时,随时计算、随时调整,大大提高了反射镜的调整效率。
反射镜调整分析
要对支撑反射镜的各个六自由度并联调整机构进行分析,必须建立相应的运动学数学模型;而数学模型是在特定坐标系下建立的,只有在坐标系下通过矩阵运算,对坐标系进行平移和旋转变换,才能针对反射镜结构建立相应的控制算法。而对反射镜位姿的调整是通过改变各双头螺杆的长度来实现的,将双头螺杆两端的虎克铰转动副的坐标作为参数添加到控制算法中,在反射镜动态调整中通过矩阵运算后测量二者之间的距离来算出每个杆件的调整量,也就是求运动学逆解的过程。
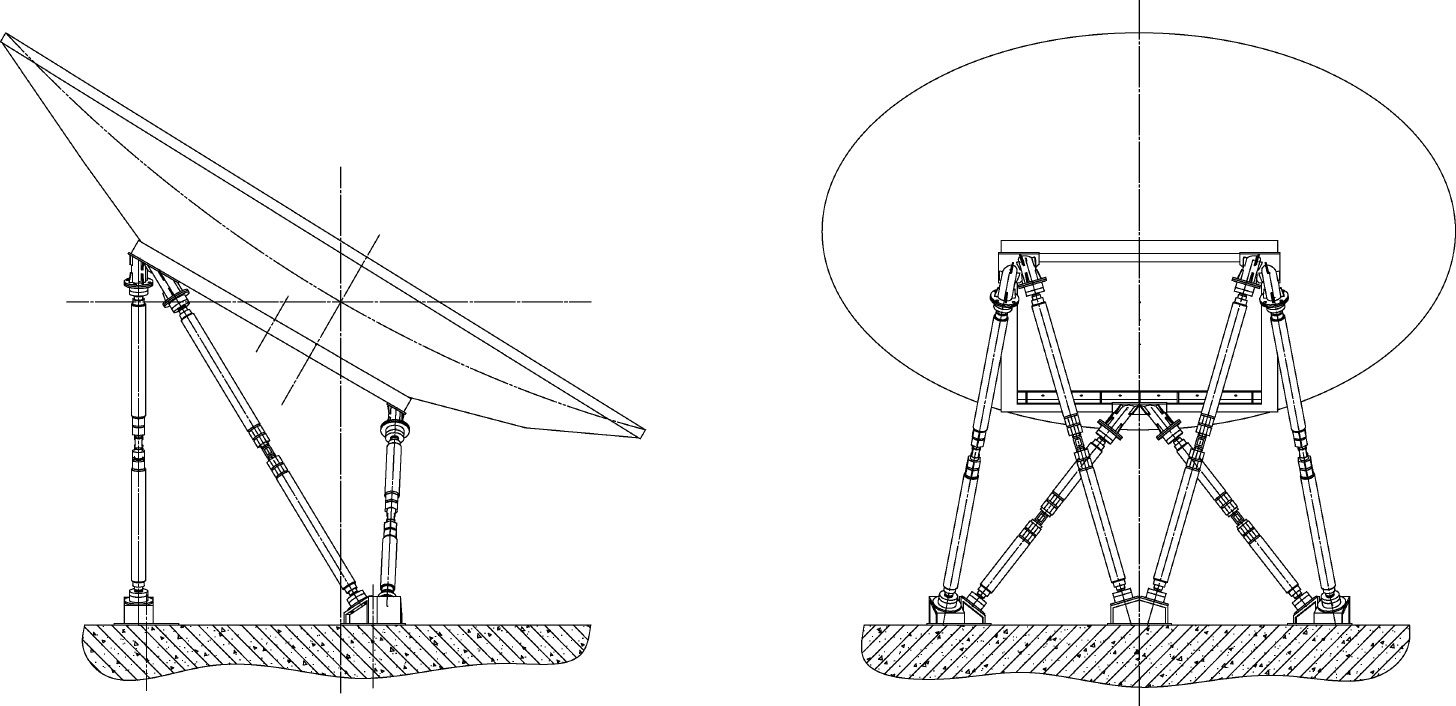
图2-41 交叉杆系调整机构结构图
反射镜调整机构的描述
以M5反射镜为例,为了便于对机构进行运动学分析,建立如图2-42所示坐标系,分为静坐标系(惯性坐标系)O-xyz和动坐标系P-uvw。其中静坐标系相对大地静止,动坐标系相对反射镜静止,可见动坐标系随着动平台(反射镜)的姿态变化而改变。

图2-42 坐标系的建立
1—反射镜;2—支链;3—双头螺杆;4—固定支座
反射镜姿态的描述
由机构自由度计算公式可知该反射镜机构具有6个自由度,反射镜的6个独立自由运动分别为相对于惯性坐标系O-xyz三个坐标轴的平移变换和旋转变换,如图2-43所示。
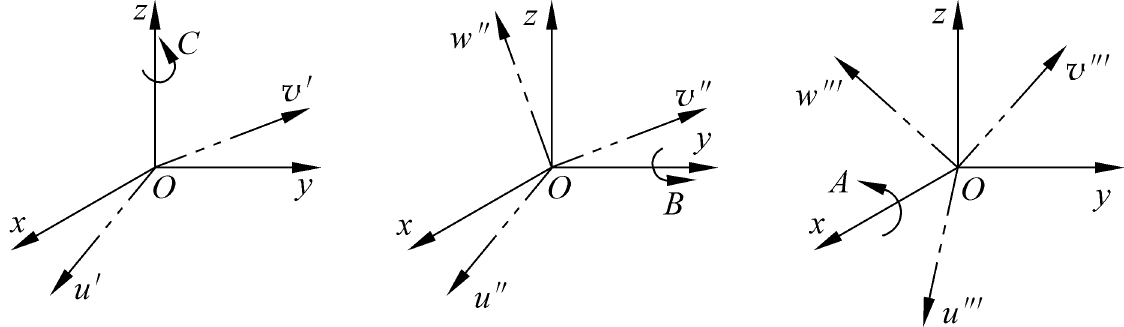
图2-43 动坐标系绕静坐标系的顺次旋转
动坐标系相对于静坐标系的旋转变换可以看作是首先使动坐标系与静坐标系重合,将动坐标系绕z轴旋转角度C得到P-u′v′w′,将P-u′v′w′绕着y轴旋转角度B得到P-u″v″w″,再将P-u″v″w″绕着x轴旋转角度A最终得到坐标系P-uvw,将各基本旋转矩阵左乘,便可以得到动坐标系P-uvw相对于静坐标系O-xyz的旋转变换矩阵Q。
Q=Rx,ARy,BRz,C
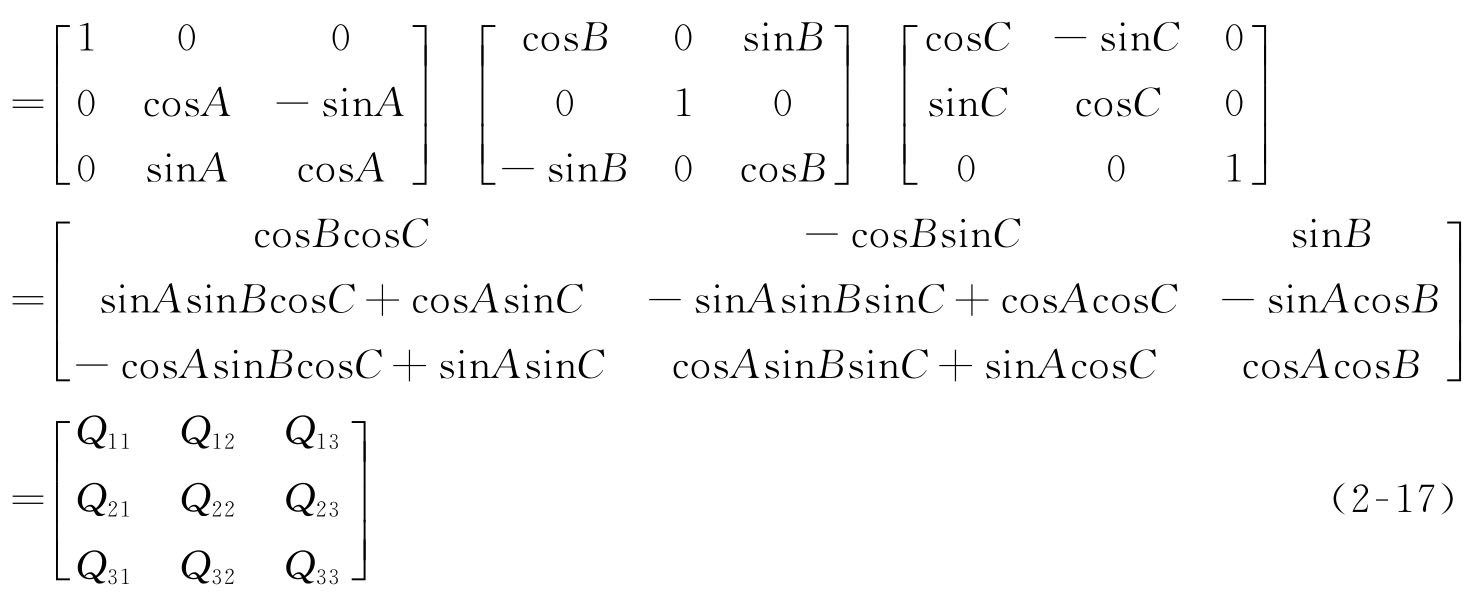
运动学模型的建立
在运动学分析中,本质是了解机构的运动特性,求解该机构的输入构件和输出构件之间的位置关系。本文分析的并联结构在运动学分析中,统一将各运动矢量在静坐标系中表达,动平台(反射镜)上各转动副Ai(i=1~6)在运动坐标系P-uvw下的位置矢量为ai,和固定支座连接的相对应的各转动副Bi在静坐标系O-xyz下的位置矢量为bi,二者的坐标变换表达式为:
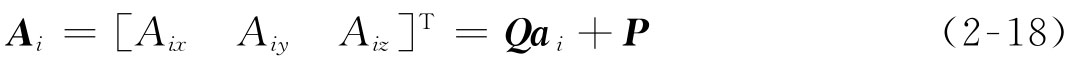
式中 Aix=Q11bix+Q12biy+Q13biz;
Aiy=Q21bix+Q22biy+Q23biz;
Aiz=Q31bix+Q32biy+Q33biz;
bi=[bix biy biz]T;
P=[X Y Z]T;
Ai——动平台上各转动副在静坐标系下的坐标;
P——从点O到点P的平移向量;
Q——从bi到ai的旋转变换矩阵。
位置逆解
并联机构的位置分析分为两种,即位置正解和位置逆解:已知各驱动构件的位置参数,求解末端执行器的位置参数,称为运动学位置正解;当已知末端执行器的位置参数,求解各输入构件的位置参数,称为位置逆解。本节分析的反射镜调整过程中,是已知反射镜的位置,求解各支撑杆件的输入量,属于求位置逆解问题。该并联机构的位置逆解可归结为:已知动平台(反射镜)的位姿即给定X、Y、Z、A、B、C,求解各支链(支撑杆件的双头螺杆)螺旋副的行程di(i=1,2,…,6),和固定支座固连的转动副bi在静坐标系下的坐标在反射镜姿态变化过程中的坐标不变。
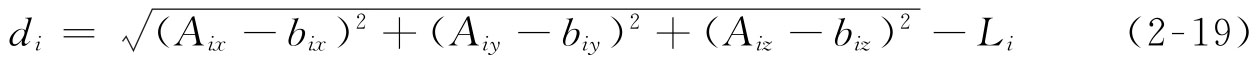
式中 Li——各支撑杆件ai与bi之间的原始长度。
反射镜调整的实现
该反射镜系统的六自由度调整机构无论是平行杆系结构还是交叉杆系结构都属于并联机构范畴。并联机构求逆解的过程比较复杂,需要多次进行矩阵转换才能求解,而且存在多个解,必须从中筛选出最优解。虽然运动学和动力学分析软件,如ADAMA、SolidWorks及COSMOS等,可以对并联机构进行运动学和动力学分析,但都不能直接求出主动件的调整量。因此在反射镜调整过程中,为了提高效率,必须自己开发相应的调整程序求解出各驱动杆件的调整量,才能实现对反射镜位姿的调整。因此在VC++6.0开发环境下,把前面建立的运动学数学模型转换为软件语言,开发出人机交互式界面,实现了反射镜的调整。
人机交互式界面开发
利用VC++6.0构建基于单文档多视图的应用程序框架。利用其中提供的各种编辑框和按钮完成界面开发,开发的界面如图2-44所示。其中,界面左上角的按钮可选择反射镜类型(平行杆系和交叉杆系),右侧的按钮可选择反射镜编号(M1~M7)。

图2-44 人机交互式界面
界面中ΔX、ΔY、ΔZ为当前反射镜位置和理论位置相比得出的平移变化量,而ΔA、ΔB、ΔC为当前反射镜坐标系(动坐标系)和惯性坐标系(静坐标系)在3个坐标系平面投影的夹角。“当前各杆长度”一栏求出的是在当前反射镜姿态下ai与bi(i=1,2,…,6)之间的距离,“与上次比较杆伸缩量”一栏可以求出在当前反射镜姿态下各支撑杆件的长度和上一次反射镜位姿调整后各支撑杆件长度比较后螺旋副di的伸缩量。
空间平面转角计算
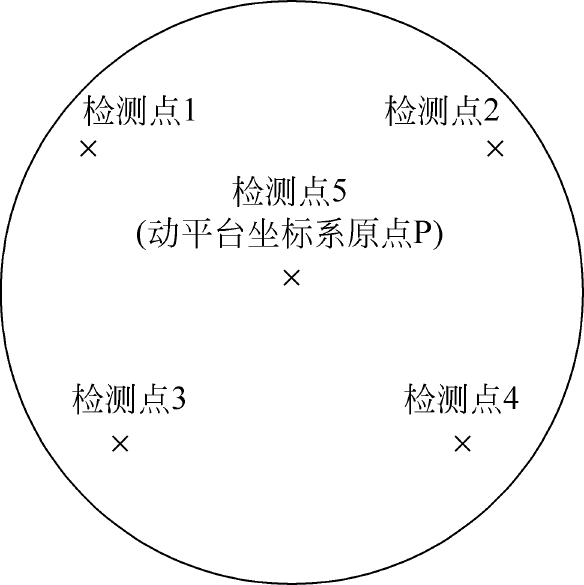
图2-45 反射镜上检测点分布图
在实际调整过程中,现有的激光跟踪仪只能测出在任意局部坐标系下检测孔上点的坐标,而无法直接给出反射镜平面与3个坐标平面的夹角,因此必须利用选定的3个检测点的坐标拟合出一个平面,再利用解析法算出空间平面与坐标平面的夹角,如图2-45所示。从5个检测点中选出3个检测点,建立三元一次方程组,便可以得出空间夹角A、B、C。
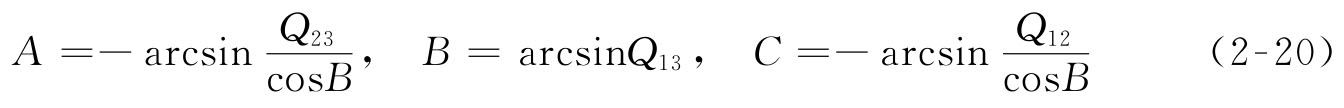
因此,当给定反射镜在设定坐标系下其中3个点的坐标(其中检测点5为动平台坐标系原点),就可以算出平移量X、Y、Z和旋转量A、B、C。
小结
通过在实际工程中的应用,验证了建立的运动学数学模型是正确的,开发的界面是有效的,但是在反射镜实际调整过程中,发现操作界面中有许多需要改进的细节,如每次都需要手动输入检测点坐标,需要增加每次调整量记录等,需要在后续工作中进一步完善。
同时,在整个反射镜调整过程中发现,由于反射镜存在安装误差,同时在调整过程中采用手动调整带来累积误差,按软件界面生成的各杆件调整量进行调整时不可能一次到位,必须经过几次调整直到软件生成的杆件调整量在允许范围内为止。若在建立的运动学数学模型中,能够利用激光跟踪仪采集到点的坐标逆向求解,推导出由于加工误差、安装误差、调整误差造成的误差公式,作为参数添加到该运动学数学模型中,将大大提高调整的精度和效率。