角度标校共分为两部分工作内容：角度标定和校准。角度标定就是对天线方位和俯仰角度零值进行标定；角度校准就是对天线系统各项轴系误差进行修正。

在一般口径的测控天线系统中，角度标校工作是通过建立标校塔、天线加装标校望远镜、建立光学坐标系，以及俯仰翻转180°进行正倒镜的光电轴标校等手段完成的（常规标校）。在DSF1中由于天线口径达到66m，建立满足距离和高度要求的标校塔是不可能的，此外俯仰翻转180°也是不现实的，因此只能利用射电星进行角度标校工作。由于射电星不断运动且信号很微弱，需要使用高灵敏度的设备，如辐射计等；此外需要大量软件完成射电星位置计算、制定观测规划、角误差数据处理、G/T值计算等工作，所以DSF1中设立专门的标校子系统完成角度标校等工作。

天线副反射面实时修正数据标定时，在天线仰角37°以下时先进行一次角度标校，其目的是为了使得天线在仰角37°以上可准确对准射电星；第二次在仰角6°~90°范围进行角度标校才是对角误差修正系数的全面标定。2次角度标校的原理和方法步骤完全一样。

射电星法角度标校原理

射电星进行角度标校的原理是以经过天文测量已精确测定位置（一般单站VLBI测试误差小于或等于0.006″，国际VLBI联合观测精度更高）的恒星为基准，对电轴进行精确标校。角度标校工作分为2步：第一步是利用射电星进行角度零值标定，第二步是利用射电星对轴系误差修正系数进行精确标定。由于射电星数量较多，每一颗星运行范围比较大，通过合理选取不同的星座及同一星座不同时刻的位置，使得射电星（信号源）均匀分布在天球上，可以确保对天线角度及轴系误差进行精确标校。

标校时，选取合适的星组，计算出星组在某一地点观测时刻的方位和俯仰角（A_真值，E_真值）；经过观测，得出某一恒星在天线观测时实际测量的方位和俯仰角（A_观测值，E_观测值），两组数据进行比较得出ΔA、ΔE。经过多次观测获得一组角误差数据（ΔA₁，ΔE₁，…，ΔA_n，ΔE_n），再采用最小二乘法处理，分解出8个误差修正系数，代入角误差修正模型，从而将系统误差修正到最小。

无论是进行角度零值标定工作，还是进行角误差修正系数标定工作，其前提都是必须选择合适的射电星组。

射电星的选择

选择合适的射电星是角度标校工作的前提。总的原则如下：

尽量选择点源

由于天线波束本身极窄，要求的指向精度在X频段达到0.01°，这就要求所选射电星的角径尽量小，否则会降低标校精度。太阳系中的金星、火星和水星的辐射都是热致辐射，其辐射接近绝对黑体，尽管它们投射到地球上的流量较弱，但由于它们都具有很小的角径，对大型天线的角度标校也是非常理想的。可供利用的部分射电星角径及其Y因子如表2-5和表2-6所示。

射电星分布均匀

首先做好观测规划，选择的射电星轨迹尽量均匀分布在天球上，即在天线工作范围内均匀选择观测点，这样可以保证得到精确的轴系误差修正参数。观测规划由标校子系统专用软件完成，其主要原理就是计算并打印出可用射电星相对于观测站东升西落的轨迹，供标校时选择使用。

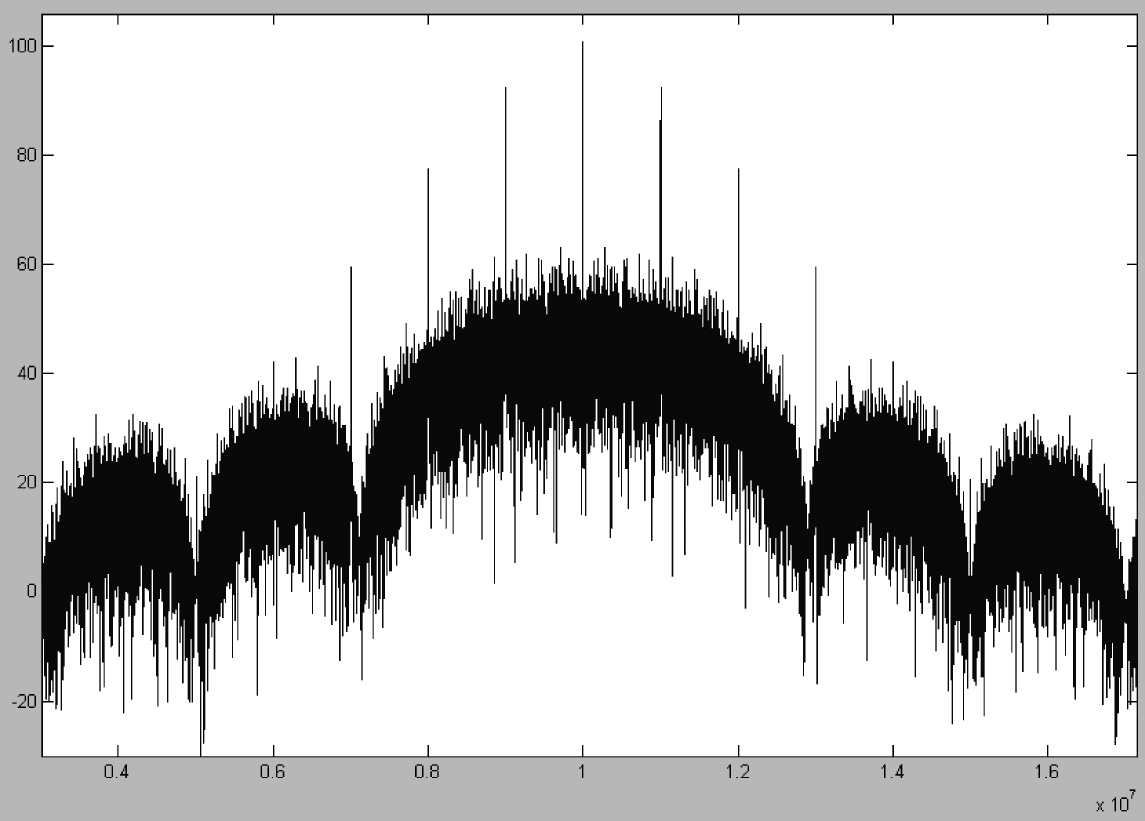
根据DSF1的天线工作频段和天线口径，所选射电星为3C273B、3C454.3、3C144（金牛座A）、3C405（天鹅座A）、3C461（仙后座A）、3C286、3C380、3C279、3C345等，利用上述射电星进行天线指向测量，得到射电星观测点在天球上的轨迹如图2-34所示。

从图中可以看出：射电星轨迹以北天极P为中心，由赤纬高的星向赤纬低的星往南排列；以这些射电星轨迹作为天线指向测量校正点用在整个天区有良好的覆盖，可以满足天线对全天区指向误差的修正。

角度零值标定

按上述原则选择好射电星后，便可首先进行角度零值标定工作。实际工作中，在进行天线副反射面调整和实时修正工作后，天线角度的零点已经初步确定，但还需要对角度零值进行精确标定工作。

角度零值精确标定选用仙后座A（Cassiopeia A）、金牛座A（Taurus A）、天鹅座A（Cygnus A）、猎户座（Orion）和Omega座等射电星，这些射电星流量密度较大，作为零值标定的信号源较为合适。

角度零值标定选用和方向图的轴线作为基准，但和方向图顶部较为平坦，同时上述各射电星的角径也较大，为找到精确的波束中心，采用五点法最为理想。在X频段其流程如图2-35所示。

按上述方法求出方位和俯仰偏差量后，还需按下述公式计算天线在某角度零值偏差：

通过对几颗星体每隔1h观测一个点，每颗星都观测一个完整弧段，对所有点的ΔA₀和ΔE₀取均值后，在角编码单元对天线零值进行修正，角度零值标定工作即告一段落，但此时的零值包含残差和轴系误差。

角误差修正

角误差修正模型

由于66m天线采用射电星法标校，所以角误差修正采用天文系统通用的修正模型：

其中：

A₁=tanecosa，A₂=tanesina，A₃=tane，A₄=-sece，A₅=1

X₁=-f_icos ka，X₂=-f_isin ka，X₃=eps，X₄=delta，X₅=Kaz

B₁=-sina，B₂=cosa，B₃=cose，B₄=ctane，B₅=1

Y₁=-f_icos ka，Y₂=-f_isin ka，Y₃=Beta，Y₄=ato，Y₅=Kel

式中　a、e——测得ΔA、ΔE时的方位角／俯仰角；

f_i——方位轴相对于天顶的偏差；

ka——方位轴偏差发生的方向；

eps——方位轴／俯仰轴非正交误差；

delta——电轴与俯仰轴非正交误差；

Kaz——方位角度零点误差；

Beta——重力变形系数；

ato——大气折射修正后的残差；

Kel——俯仰角度零点误差。

角误差修正系数的标定

角误差修正系数的标定采用五点法或扫描法都可以实现，其最终目的都是根据计算出的射电星位置和观测到的射电星位置得出两者之间的差异（ΔA、ΔE）。标校时选取合适的星组，利用标校计算机中的专用软件计算出星组在某一地点观测时的方位和俯仰角，即（A_真值，E_真值），经过观测得出某一恒星在天线观测时实际测量的方位和俯仰角（A_量值，E_量值），2组数据进行比较得出ΔA、ΔE。经过中国科学院有关专家多年研究，可以用这一测试方法分解出上述公式中8个误差项，将系统误差动态修正到最小。其基本原理如下。

当天线在某一角度时，其观测角度与真值的误差由几方面组成，即：

式中　ΔA₁——方位零值误差；

ΔA₂——方位轴倾斜引起的方位误差；

ΔA₃——方位轴与俯仰轴不正交引起的方位误差；

ΔA₄——电轴与俯仰轴不正交引起的方位误差；

ΔE₁——俯仰零值误差；

ΔE₂——方位轴倾斜引起的俯仰误差；

ΔE₃——天线重力下垂引起的俯仰误差；

ΔE₄——大气折射修正后的残差。

当式中各项误差都很小时有

方位轴不垂直误差：

方位轴和俯仰轴不正交误差：

电轴与俯仰轴不正交误差：

天线重力下垂误差：

设有n个观测量ΔA₁~ΔA_n、ΔE₁~ΔE_n，它们均为未知参量f_i、ka、eps、delta、Kaz、Beta、ato、Kel的线性函数，将这n个误差量代入式（2-4）和式（2-5），建立n个方程式，便能求出上述8个未知参量。如果选择不同的射电星，它们在空中分布均匀而且覆盖的天区又比较大，进行多次测量后宜用最小二乘法来处理这些观测结果，求出以上各参量的最似然值。

根据天线指向模型的公式，将得到的A_计算值、ΔA和E_计算值、ΔE这2组数据换算成为最小二乘法计算所需要的数据，换算方式如下：对于方位轴，设

对于俯仰轴，设

再根据最小二乘法的矩阵解法得到如下方程式：

得出关于方位轴的模型系数值为[X]=[a₁ a₂ a₃ a₄ a₅]\[b]，俯仰轴的模型系数值为[X]=[a₁ a₂ a₃ a₄]\[b]。

在实际的标校工作中，角误差修正系数的求解也是由标校计算机中专用软件来完成的，只需将观测数据（A_计算值1，ΔA₁）、（E_计算值1，ΔE₁）、…、（A_计算值n，ΔA_n）、（E_计算值n，ΔE_n）导入误差处理软件即可解算出各项轴系误差修正系数。