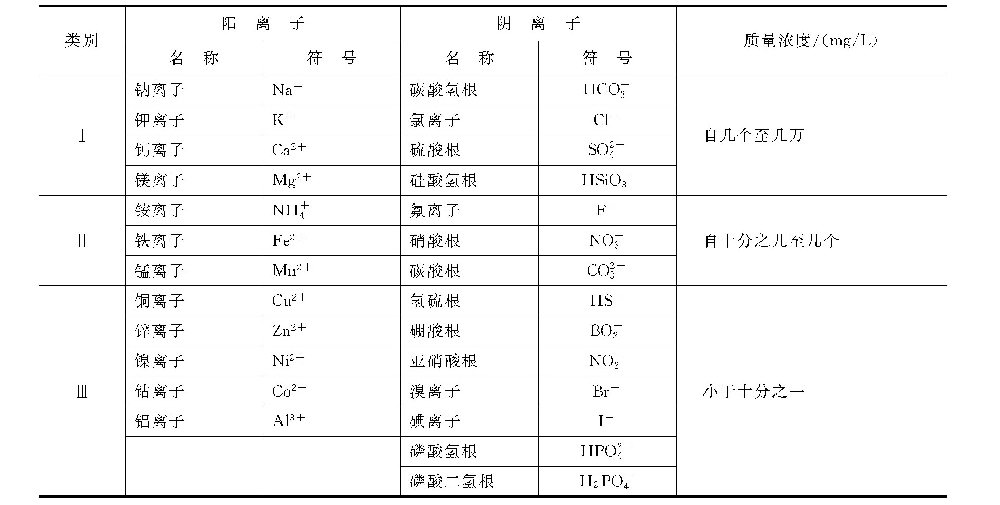
假设循环冷却水系统为连续补充水和连续排污，其水量基本稳定。并假设水中溶解离子浓度的变化与大气无关，冷却水中某些能导致结垢的离子浓度在使用阻垢分散剂所允许的极限浓度范围之内，不析出沉积。这样，溶解离子只由补充水带入，只从排污水带出。在运行一段时间之后，浓缩倍数会达到一个稳定值，因而水中溶解离子也基本稳定在一定浓度。

运行过程中由于各种原因有时需要提高或降低浓缩倍数，调整补充水或排污水量，则会引起水中溶解离子浓度的变化，其关系式为：

式中 V———系统容积或保有水量，m³；

B———排污水量（包括渗漏、风吹损失水量），m³/h；

C_M———某离子在补充水中的质量浓度，mg/L；

C₀———某离子在循环冷却水中的初始质量浓度，mg/L；

C———某离子在循环冷却水中变化后的质量浓度，mg/L；

t₀———形成C₀时的时刻，H；

t———形成C时的时刻，H；

N———要求达到的浓缩倍数；

e———自然对数底数，约为2.718。

当NC_M>C₀时，离子浓度增高，为浓缩过程。当NC_M<C₀时，离子浓度降低，为稀释过程。

用该关系式可以大致计算出从冷态运行到一定浓缩倍数所需的时间。例如，某系统容积为4800m³，排污水量为480m³/h，补充水中氯离子为50mg/L，该系统未使用氯型杀生剂，故氯离子浓度只受浓缩影响，无其他增加因素，要求计算从冷态运行达到3倍时大约所需时间。

冷态时C_M＝C₀＝50mg/L，t－t₀＝5H时，C＝3×50－（3×50－50）e^{－480×5/4800}＝150－100e^－0.5＝89.4mg/L，按此法计算的t－t₀与氯离子质量浓度C的关系如下表：

由该式计算结果，浓缩到N＝3时，时间为无穷长。如果取达到0.95 N时的时间，即C＝142.5mg/L时，约为25～30H。

用该式也可计算降低浓缩倍数所需的大致时间。例如系统容积为2000m³的系统，补充水的钙离子质量浓度为40mg/L。该系统已浓缩至5倍，即循环水中钙离子为200mg/L。为减少碳酸钙结垢倾向，希望将钙离子降至160mg/L，即4倍。如果排污水量为220m³/h，计算降至4倍大约需要的时间。

t－t₀＝5H时，C＝4×40－（4×40－200）e^{－220×5/2000}＝160＋40e^－0.55＝183.1mg/L，不同t－t₀与钙离子质量浓度C的关系如下表：

该式计算结果达到4倍时，时间也为无穷长，如取达到4.05倍，即钙离子为162mg/L的时间，则约需25～30H。