计算机只能识别二进制数，而要求计算机处理的数，如无符号数、有符号数等，又种类繁多，怎么办呢？计算机中采用各种形式的编码很好地解决了数及字符等信息的表示问题。

数据可分为两大类：数值数据和非数值数据。前者表示数量的多少；后者表示字符、汉字、图形、图像、声音等，又称符号数据。在计算机内，无论哪一种数据，都以二进制形式表示。本节首先讲解数值数据在计算机中的表示方法。

数据的单位

计算机中数据的常用单位有位、字节和字。

位（Bit）

计算机中最小的数据单位是二进制的一个数位，简称为位（英文名称为Bit，读音为比特）。计算机中最直接、最基本的操作就是对二进制位的操作。

字节（Byte）

字节这个词是在1956年左右由IBM公司最早提出来的。这个词起源于Bite，但用y代替了i，以避免被人误认为它是Bit，也就成了现在的Byte。曾经有一段时期，字节仅仅简单地表示特定数据路径上数据的位数。但是到了20世纪60年代中期，随着IBM的360系统的发展，字节这个词专门用来表示8位二进制数。

作为一个8位二进制数，一个字节可以从00000000取值到11111111。这些数可以代表0～255的正数，也可以表示−128～127范围之内的正、负数。总之，一个特定的字节可以代表2⁸（即256种）不同事物中的一个。

字节简写为B，它是计算机中用来表示存储空间大小的基本容量单位。

与字节有关的常用换算单位如下：

1B＝8bit；1KB＝1024B＝2¹⁰B；1MB＝1024KB＝2¹⁰KB＝2²⁰B；1GB＝1024MB＝2¹⁰MB＝2³⁰B；1TB＝1024GB＝2¹⁰GB＝2⁴⁰B；1PB＝1024TB＝2¹⁰TB＝2⁵⁰B；1EB＝1024PB＝2¹⁰PB＝2⁶⁰B。

字（Word）

在计算机中作为一个整体被存取、传送、处理的二进制数字符串叫作一个“字”或“单元”。每个字中二进制位数的长度，称为字长。

一个字由若干个字节组成，不同的计算机系统的字长是不同的，常见的有8位、16位、32位、64位等。字长越长，计算机一次处理的信息位就越多，精度就越高。字长是计算机性能的一个重要指标。目前大部分计算机都是32位的。

在汇编语言程序中，字为16位二进制数，即1Word＝2Byte＝16bit；把32位二进制数，即两个字称为双字（Double Word）。

定点数表示方法

在选择计算机数值的表示方式时，需要考虑以下几个因素：①要表示的数的类型（小数、整数、实数和复数）；②可能遇到的数值范围；③数值精确度；④数据存储和处理所需要的硬件代价。

计算机处理的数值数据多数带有小数。小数点在计算机中通常有两种表示方法：一种是约定所有数值数据的小数点隐含在某一个固定位置上，称为定点表示法，简称定点数；另一种是小数点位置可以浮动，称为浮点表示法，简称浮点数。

所谓定点数，就是约定计算机中所有数据的小数点位置是固定不变的。在计算机中通常采用两种简单的约定：将小数点的位置固定在数据的最高位之前，或者是固定在最低位之后。一般常称前者为定点小数，后者为定点整数。

定点小数

定点小数约定的小数点位置在符号位之后、有效数值部分最高位之前，即一个数的最高二进制位是符号位，用来表示数的符号，而小数点的位置默认为在符号位后面，不单独占一个二进制位。

例如，数据x的形式为x＝x₀.x₁x₂…x_n（其中，x₀为符号位，x₁～x_n是数值的有效部分，也称为尾数，x₁为最高有效位），则x在计算机中的表示形式为：

所以，在一个定点小数中，符号位右边的所有二进制位数表示的是一个纯小数。

定点整数

定点整数约定小数点位置在有效数值部分最低位之后，即一个数的最高二进制位是符号位，用以表示数的符号；而小数点的位置默认为在最低（即最右边）的二进制位的后面，但小数点不单独占一个二进制位。

例如数据x的形式为x＝x₀x₁x₂…x_n（其中，x₀为符号位，x₁～x_n是尾数，x_n为最低有效位），则x在计算机中的表示形式为：

所以，在一个定点整数中，符号位右边的所有二进制位数表示的是一个纯整数。

浮点数表示方法

在计算机中，定点数通常只用于表示纯整数或纯小数，而对于既有整数部分又有小数部分的数，由于其小数点的位置不固定，一般用浮点数表示。

计算机中所说的浮点数就是指小数点位置不固定的数。一般地，一个既有整数部分又有小数部分的十进制数D可以表示成如下形式：

D ＝ R×10^N

式中，R为一个纯小数；N为一个整数。

例如，一个十进制数123.456可以表示成0.123456×10³，十进制小数0.00123456可以表示成0.123456×10⁻²。纯小数R的小数点后第一位一般为非零数字。

同样，对于既有整数部分又有小数部分的二进制数也可以表示成如下形式：

D ＝ R×2^N

式中，R为一个二进制定点小数，称为D的尾数；N为一个二进制定点整数，称为D的阶码，它反映了二进制数D的小数点的实际位置。

为了使有限的二进制位数能表示出最多的数字位数，定点小数R的小数点后的第一位（即符号位的后面一位）一般为非零数字（即为“1”）。

原码的表示方法

二进制数跟十进制数一样也有正负之分。在计算机中，常采用数的符号和数值一起编码的方法来表示数据。常用的有原码、反码、补码、移码等。这几种表示法都将数据的符号数码化。为了区分一般书写时表示的数和机器中编码表示的数，我们称前者为真值，后者为机器数或机器码。

所谓原码就是前面所介绍的二进制定点数表示法，即最高位为符号位，“0”表示正，“1”表示负，其余位表示数值的大小。

定点小数的原码

假设定点小数的原码形式为x₀.x₁x₂…x_n，则其原码表示的定义为

式中，［x］_原是机器数；x是真值。

例如，x ＝ ＋0.1001，则［x］_原 ＝ 0.1001

定点整数的原码

假设定点整数的原码形式为x₀x₁x₂…x_n，则其原码表示的定义为

原码表示法的优点是比较直观、简单易懂，但它的最大缺点是加法运算复杂。这是因为，当两数相加时，如果是同号则数值相加；如果是异号，则要进行减法。而在进行减法时，还要比较绝对值的大小，然后减去小数，最后还要给结果选择恰当的符号。显然，利用原码做加减法运算是不太方便的。为了解决这些矛盾，人们找到了补码表示法。

补码的表示方法

由于计算机的运算受一定字长的限制，属于有模运算，所以，在计算机中可以使用补码进行计算。在定点小数机器中，数最大不超过1，也就是负的小数对“1”的补码是等价的。但实际上，负数的符号位还有一个“1”，要把它看成数的一部分，所以要对2求补码，也就是以2为模数。

定点小数的补码

假设定点小数的补码形式为 x₀. x₁x₂…x_n，则其补码表示的定义为

对于0，在补码情况下只有一种表示形式，即

［＋0］_补 ＝ ［−0］_补＝0.000…0

定点整数的补码

假设定点整数的补码形式为 x₀ x₁x₂… x_n，则其补码表示的定义为

采用补码表示法进行减法运算就比原码方便多了。因为不论数是正还是负，机器总是做加法，减法运算可变成加法运算。但根据补码定义，正数的补码与原码形式相同，而求负数的补码要减去|x|。为了用加法代替减法，结果还得在求补码时做一次减法，这显然是不方便的。从下面介绍的反码表示法中可以获得求负数补码的简便方法，解决负数的求补问题。

反码的表示方法

反码表示法中，符号的表示法与原码相同。正数的反码与正数的原码形式相同；负数的反码符号位为1，数值部分通过将负数原码的数值部分各位取反（0变1，1变0）得到。

定点小数的反码

假设定点小数的反码形式为 x₀. x₁x₂…x_n，则其反码表示的定义为

对于0，在反码情况下只有两种表示形式，即

［＋ 0］_反 ＝ 0.000…0 ［− 0］_反 ＝ 1.111…1

定点整数的反码

假设定点整数的反码形式为x₀ x₁x₂…x_n，则其反码表示的定义为

移码的表示方法

移码通常用于表示浮点数的阶码。阶码是个n位的整数，假设定点整数移码形式为x₀ x₁x₂… x_n时，移码的定义为

由移码的定义式可知，对于同一个整数，其移码与其补码数值位完全相同，而符号位正好相反。

将十进制真值x＝−127、−1、0、＋1、＋127分别表示为8位原码、反码、补码、移码值的结果见表1-2。

表1-2　原码、反码、补码、移码值举例

BCD码的表示方法

计算机中使用的是二进制数，人们习惯使用的是十进制数，因此，输入到计算机中的十进制数需要转换成二进制数；数据输出时，应将二进制数转换成十进制数。为了方便，大多数通用性较强的计算机需要能直接处理十进制形式表示的数据。为此，在计算机中还设计了一种中间数字编码形式，它把每一位十进制数用4位二进制编码表示，称为二进制编码的十进制表示形式，简称BCD码（Binary Coded Decimal），又称为二-十进制数。

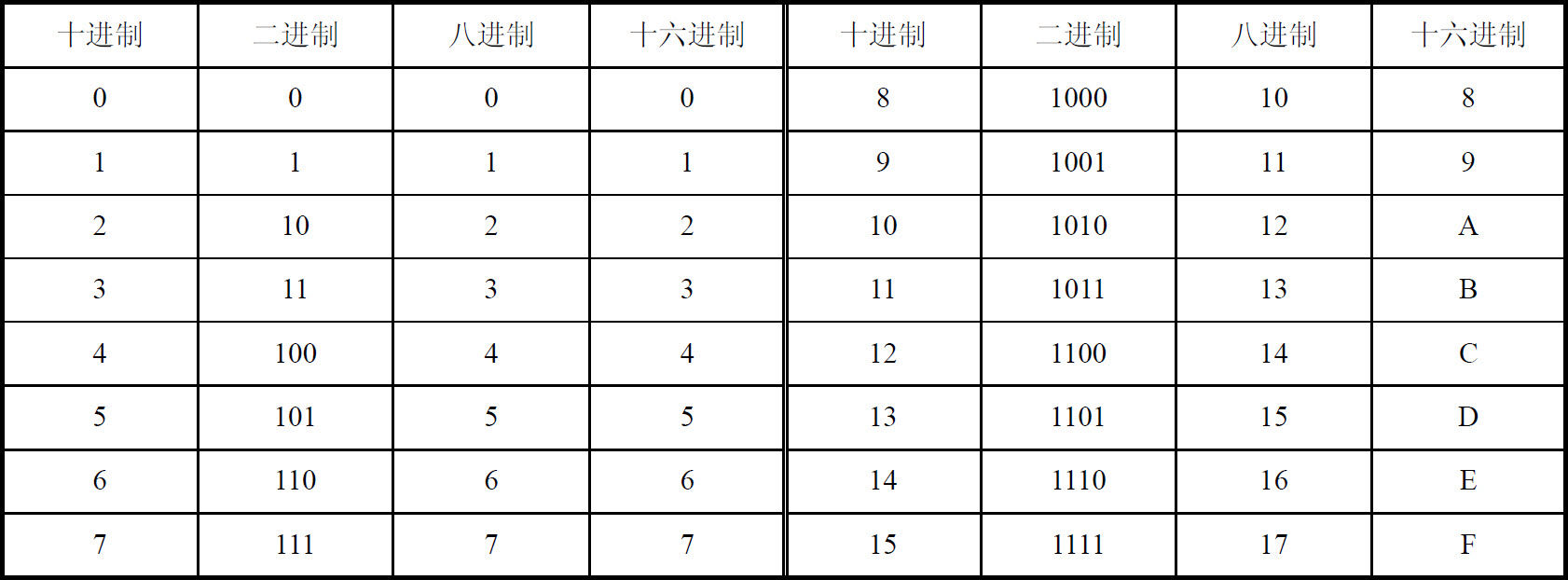
4位二进制数码，可编码组合成16种不同的状态，而十进制数只有0、1、…、9这十个数码，因此选择其中的十种状态做BCD码的方案有许多种，如8421BCD码、格雷码、余3码等。编码方案见表1-3。

表1-3　常用BCD编码对照表

最常用的BCD码是8421BCD码。8421BCD码选取4位二进制数的前10个代码分别对应表示十进制数的10个数码，1010～1111这6个编码未被使用。从表1-2中可以看到这种编码是有权码。4个二进制位的位权从高向低分别为8、4、2和1。若按权求和，和数就等于该代码所对应的十进制数，例如0110＝2²＋2¹＝6。

把一个十进制数变成它的8421BCD码数值，仅对十进制数的每一位单独进行即可。例如变1986为相应的8421BCD码表示，结果为0001 1001 1000 0110。反转换过程也类似，例如变0101 1001 0011 0111为十进制数，结果应为5937。