数据（Data）是表示客观事物的、可以被记录的、能够被识别的各种符号，包括字符、符号、表格、声音和图形、图像等。简言之，一切可以被计算机加工、处理的对象都可以被称为数据。数据可在物理介质上记录或传输，并通过外围设备被计算机接收，经过处理而得到结果。

进位计数制

在日常生活中，人们习惯于用十进制计数。但是，在实际应用中，还使用其他的计数制，如二进制、十二进制、二十四进制、六十进制等。用数字符号排列，由低位向高位进位计数的方法叫作进位计数制，简称进位制。进位计数制的特点是由一组规定的数字来表示任意的数。例如，一个二进制数只能用0和1来表示，一个十进制数只能用0、1、2、…、9来表示，一个十六进制数用0、1、2、…、9和A～F十六个数字符号来表示。

数据无论使用哪种进位制，都涉及两个基本要素：“基数”与各数位的“位权”。

一种计数制允许选用基本数字符号（数码）的个数叫基数。在基数为J的计数制中，包含J个不同的数字符号，每个数位计满J就向高位进1，即“逢J进一”。例如最常用的十进制中，每一位上允许选用0、1、2、…、9共10个不同数码中的一个，则十进制的基数为10，每位计满10时向高位进一。

一个数字符号处在不同位时，它所代表的数值是不同的。每个数字符号所表示的数值等于该数字符号值乘以一个与数码所在位有关的常数，这个常数叫作“位权”，简称“权”。位权的大小是以基数为底，数码所在位置的序号为指数的整数次幂。例如，十进制数的百分位、十分位、个位、十位、百位、千位的权依次是10⁻²、10⁻¹、10⁰、10¹、10²、10³。整数部分的个位位置的序号是0。

J进制数每位的值等于该位的权与该位数码的乘积。一个J进制可以写成按权展开的多项式和的形式，一个J进制数（S）_J按权展开的多项式和的一般表达式为：

式中，n是J进制数整数部分的位数；m是J进制数小数部分的位数；k_i是第i位上的数码，也称系数；Jⁱ是第i位上的权。在整数部分，i是正数；在小数部分，i应是负数。

可以看出，J进制数相邻两个数的权相差J倍，如果小数点向左移一位，数缩小J倍；反之，小数点右移一位，数扩大J倍。

二进制

计算机是由电子元器件组成的。考虑到经济、可靠、容易实现、运算简便、节省元器件等因素，在计算机中的数都用二进制表示而不用十进制表示。

二进制有如下优点：

技术容易实现

二进制计数只需要两个数字符号0和1。在电路中可以用两种不同的状态——低电平（0）和高电平（1）来表示，其运算电路的实现比较简单，并且数据的存储和传送也可用简单而可靠的方式进行；而要制造有10种稳定状态的电子器件分别代表十进制中的10个数字符号是十分困难的。

二进制运算规则简单

十进制两个一位数的“和”与“积”的结果各有55种，而二进制两个一位数的“和”与“积”分别只有3种结果。所以二进制数在编码、计数和算术运算方面规则简单，容易用开关电路实现，为提高计算机的运算速度和降低实现成本奠定了基础。

逻辑运算方便

由于二进制数码的两个基本符号“0”和“1”，能方便地与逻辑命题的“否”和“是”，或称“假”和“真”相对应，为计算机中的逻辑运算和程序中的逻辑判断提供了便利条件。

二进制的基数为2，只有“0”和“1”两个数码，计数逢二进一。第i位上的位权是2的i次幂。一个二进制数展开成多项式和的表达式是：

例如：

八进制数与十六进制数

在计算机内部，一切信息的存储、处理与传送均采用二进制的形式。但由于二进制数写起来很长，且很难记，为方便起见，人们编写程序或书写指令时，通常采用八进制数或十六进制数。

八进制数基数为8，有0、1、2、3、4、5、6、7，共8个数码，逢八进一，第i位上的位权是8的i次幂。一个八进制数展开成多项式和的表达式是：

十六进制数基数为16，有0、1、2、3、4、5、6、7、8、9及大写英文字母A、B、C、D、E、F（数码A～F对应十进制数分别是10～15）共16个数码，逢十六进一，第i位上的位权是16的i次幂。一个十六进制数展开成多项式和的表达式是：

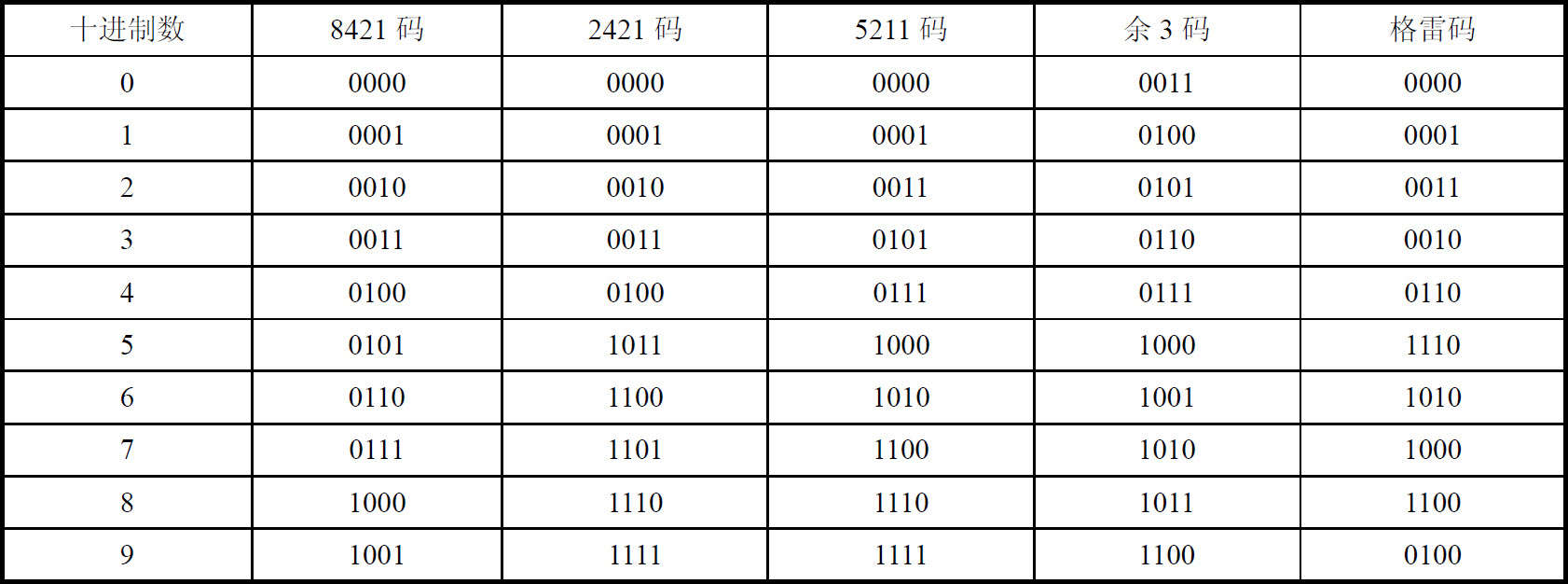
十六进制和八进制与二进制之间有着非常简单的对应关系，表1-1给出了四种常用计数制的对照表。

表1-1　四种常用计数制的对照表

进位计数制的相互转换

为了清晰方便起见，常在数字后面加字母B（Binary）表示二进制数；加O（Octal）表示八进制数，为避免把字母O误认为数字0，本书暂时改用Q字母；加H（Hexadecimal）表示十六进制数，加D（Decimal）或不加字母表示十进制数。

二进制转换成十进制

将二进制转换成十进制，只需把二进制数写成按权展开多项式和的形式，再计算此表达式的和即可。

例如，

十进制整数转换成二进制整数

将十进制整数转换成二进制整数采用“除2取余法”。即将十进制整数除以2，得到一个商和一个余数；再将商除以2，又得到一个商和一个余数；以此类推，直到商等于零为止。

每次得到的余数的倒排列，就是对应二进制数的各位数。

例如，将十进制数153转换成二进制数：

即　

十进制小数转换成二进制小数

十进制小数转换成二进制小数是用“乘2取整法”。即用2逐次去乘十进制小数，将每次得到的积的整数部分按各自出现的先后顺序依次排列，就得到相对应的二进制小数。

例如，把十进制小数0.7875转换成二进制数：

即　

如果一个十进制数既有整数部分又有小数部分，可将整数部分和小数部分分别进行J进制的等值转换，然后合并就可得到结果。

八进制转换为二进制

将八进制数转换成二进制数，每位八进制数用3位二进制数表示即可。

例如，八进制数617.34Q转换成二进制数：

即617.34Q＝110001111.011100B。

（5）二进制转换为八进制

二进制数转换成八进制数，是将二进制数的整数部分从右向左每3位一组，每一组为一位八进制整数。

二进制小数转换成八进制小数是将小数部分从左至右每3位一组，每一组是一位八进制的小数。若整数和小数部分的最后一组不足3位时，则用0补足3位。

例如，把二进制数11010110110.1001转换成八进制数：

即　11010110110.1001B＝3266.44Q。

十六进制转换为二进制

由于2⁴＝16，所以每一位十六进制数要用4位二进制数来表示，也就是将每一位十六进制数表示成4位二进制数。

例如，将十六进制数3A65.B2H转换成二进制数：

即3A65.B2H＝11101001100101.1011001B。

二进制转换为十六进制

将二进制数转换成十六进制数是将二进制数的整数部分从右向左每4位一组，每一组为一位十六进制整数；而二进制小数转换成十六进制小数是将二进制小数部分从左向右每4位一组，每一组为一位十六进制小数。最后一组不足4位时，应在后面用0补足4位。

例如，二进制数1010101011.0110B转换成十六进制数：

即（1010101011.0110）₂＝（2AB.6）₁₆，或写为1010101011.0110B＝2AB.6H。