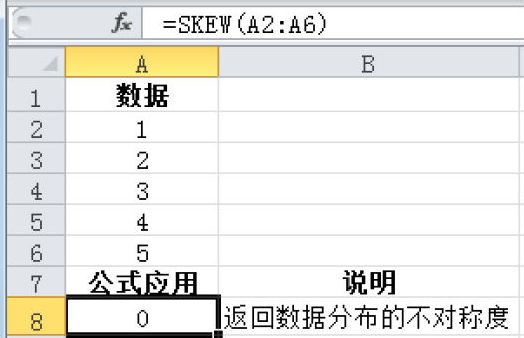
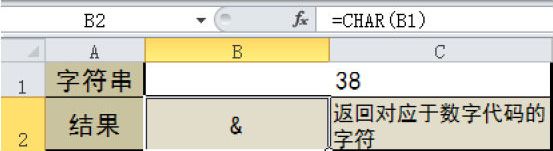
SKEW函数用于计算分布的不对称度。不对称度反映以平均值为中心的分布的不对称程度。正不对称度表示不对称部分的分布更趋向正值，负不对称度表示不对称部分的分布更趋向负值。SKEW函数的语法如下。

SKEW(number1,number2,...)

其中参数number1，number2...为需要计算偏斜度的1到255个参数。对于参数的表示也可以不使用这种用逗号分隔参数的形式，而用单个数组或对数组的引用。

典型案例

给定一组数据，计算其分布的不对称度。基础数据如图16-159所示。

步骤1：打开例子工作簿“SKEW.xlsx”。

步骤2：在单元格A13中输入公式“=SKEW（A2：A11）”，用于计算给定数据集分布的不对称度。计算结果如图16-160所示。

图16-159　基础数据

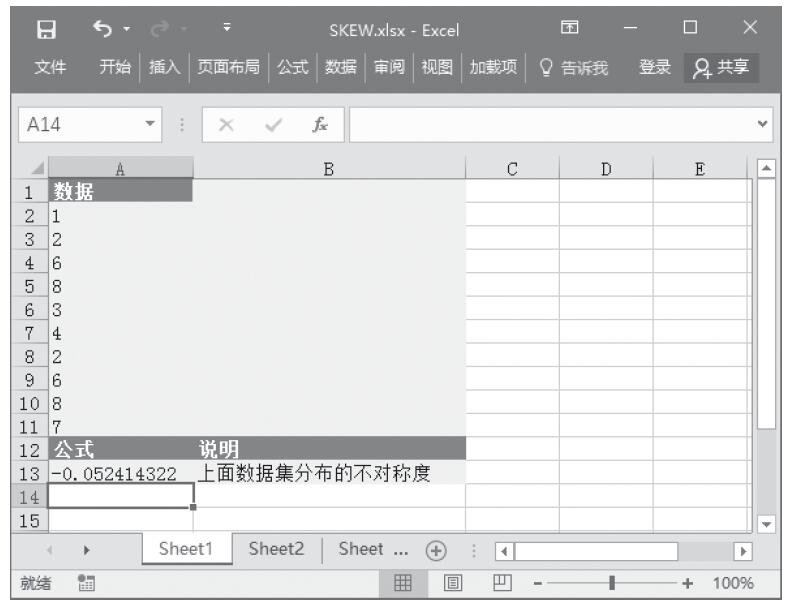
图16-160　计算结果

使用指南

参数可以是数字或者是包含数字的名称、数组或引用。逻辑值和直接键入到参数列表中代表数字的文本被计算在内。如果数组或引用参数包含文本、逻辑值或空白单元格，则这些值将被忽略，但包含零值的单元格将计算在内。

如果参数为错误值或为不能转换为数字的文本，将会导致错误；如果数据点个数少于3个，或样本标准偏差为零，函数SKEW返回错误值“#DIV/0！”。不对称度的计算公式定义如下。