交流铁心线圈电路：电磁关系与功率损耗

加正弦交流电压的铁心线圈电路如右图所示。由于铁心的存在，线圈电路既要符合电路的规律，亦要符合磁路的规律。

电磁关系

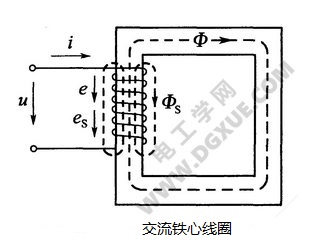当铁心线圈加入交流电压u后，即有交流电流i，线圈中便产生交变磁通。由于铁心的导磁率比空气大得多，故绝大部分磁通通过铁心闭合，这部分磁通称主磁通，又称工作磁通，记作Φ。也有一小部分磁通通过空气闭合，这部分磁通称漏磁通，记作少Φs。依电磁感应定律，变化的主磁通Φ产生的主磁电动势e为：

$$e\tag{1}\label{1}=-N\frac{d\Phi }{dt}$$

而漏磁通Φs主要通过空气闭合，励磁电流i和漏磁通Φs之间是线性关系，可用漏磁电感$L_{s}=N\Phi _{s}/i$来表示其关系，Ls是一个常数。故漏磁电动势$e_{s}$可写为：

$$e\tag{2}\label{2}_{s}=-N\frac{d\Phi _{s}}{dt}=-L_{s}\frac{di}{dt}$$

主磁通Φ是通过铁心的，由于铁心的导磁率μ不是常数， 即励磁电流i和主磁通Φ之间不是线性，所以无法用一个电感常数L来表达，即主磁电动势e无法用式上式$\eqref{2} $的形式表示， 只能用式$\eqref{1}$ 表示。

考虑到线圈导线存在很小的电阻r，所以线圈电路有电压相量方程式：

$$\dot{U}=r\dot{I}+(-\dot{E}_{s})+(-\dot{E})=r\dot{I}+jX_{s}\dot{I}+(-\dot{E})$$

式中$X_{s}=\omega L_{s}$称为漏磁电抗。由于Φs很小，故$L_{s},X_{s}$亦很小，线圈的r也很小，故式上式简化为$\dot{U}=(-\dot{E})$。数值上写为E≈U（有效值）。

设磁通Φ=Φ_msinωt，产生的感应电动势：

$$ \begin{align}e & =-N\frac{d\Phi }{dt}=-N\frac{d\Phi _{m}sin\omega t}{dt}\\ & =-N\omega \Phi _{m}cos\omega t=E_{m}sin(\omega t-90^{\circ})\end{align}$$

式中$E_{m}=\omega N\Phi _{m}$为最大值，其有效值则为：

$$E=E_{m}/\sqrt{2}=\omega N\Phi _{m}/\sqrt{2}=2\pi fN\Phi _{m}/\sqrt{2}$$

当U≈E时，有：

$$U\tag{3}\label{3}\approx E=4.44fN\Phi _{m}$$

上式建立了交流铁心线圈磁通Φ与端电压U的关系式，是很常用的公式。按上式求出Φm后，再按Bm=Φm/A，求出Bm。由Bm值查磁化曲线图确定Hm。最后根据式Hl=IN，$I_{m}=H_{m}l/N$求出电流幅值Im，其有效值$I=I_{m}/\sqrt{2}$。

当计算出来的Bm值不是处于磁化曲线的饱和区时，由于导磁率μ很大，故磁场强度—是很小的，即励磁电流是很小的。反之，当Bm值处于磁化曲线饱和段时，μ值很小， 此时Hm显著加大，励磁电流亦显著加大。通常铁心线圈设计其值处于临近饱和段前的拐弯点处，此时最经济。但此时若交流电压U波动20%，则按式$\eqref{3} $，Φm亦波动20%，Bm波动20%而引起的Hm及Im却由于工作在磁化曲线饱和段而增加几倍。即交流铁心线圈的电流对电压上波相当敏感。其后果可能烧坏线圈。

练一练

问题：要绕制一个铁心线圈，已知交流电压U=220V，f=50Hz。现有硅钢片铁心，截面积为30.2cm2,磁路平均长度l=60cm，设叠片间隙系数为0.91 (—般取0.9~0.93)。求：若取Bm为1.2T时，线圈该绕多少匝？又此时励磁电流I是多少？

解题：铁心的有效面积为叠片系数与测量截面积之乘积。

A=0.91×30.2=27.5cm²

①：根据式$\eqref{3} $，求出线圈匝数为300匝。

$$N=\frac{U}{4.44fB_{m}}A=\frac{220}{4.44\times 50\times 1.2\times 27.5\times 10^{-4}}=300$$

②：由Bm=1.2T查磁化曲线图，得Hm=650A/m，故励磁电流I为：

$$I=\frac{H_{m}l}{\sqrt{2}N}=\frac{650\times 60\times 10^{2}}{\sqrt{2}\times 300}=0.92A$$

功率损耗

交流铁心线圈的功率损耗包括铜损和铁损两部分，其中铁损又包括磁滞损耗和涡流损耗两种。分述如下：

一、铜耗：它是电流流过线圈电阻r的损耗△P_Cu

$$\Delta P_{Cu}=rI^2$$

二、磁滞损耗：磁滞损耗。它是由于铁心交变磁化时的磁滞现象所产生的损耗。实验证明，单位体积磁滞损耗的大小与磁滞回线所包围的面积成正比，所以，为减少磁滞损耗，应选用磁滞回线狭小的软磁材料做铁心。磁滞损耗△P_h为：

$$\Delta P_{h}=K_{h}fB^{n}_{m}V$$

公式中：

• K_h——磁滞损失系数，与材料有关，可查相关手册；
• f——频率，Hz；
• B_m——磁感应强度，T；
• V——铁心体积，m³
• n——与B_m值有关的指数。

$$n=\left\{\begin{matrix}1.6(B_{m}=0.1\sim 1.0T)\\
2(0.1T> B_{m},B_{m}> 1.0T)
\end{matrix}\right.$$

三、涡流损耗：交变磁通穿过铁心内部，在铁心内部垂直磁通的横断面上产生感应电动势，铁心本身又是导电的，该电动势在铁心的横断面上形成的电流，称为涡流。涡流流过铁心，铁心本身的电阻便会产生热损耗，为减小涡流损耗，所以采用片状磁性材料叠成铁心，片间彼此绝缘，使涡流在薄片的横断面内流动，由于涡流路径增长，电阻增大，电流变小，因而损耗减小。另外，在铁磁材料中加人少量的硅，可使其电阻率显著增加。铁心材料常采用硅钢片。涡流损耗△P_e为：

$$\Delta P_{e}=K_{e}f^{2}B^{2}_{m}V$$

式中，Ke——与铁心导电系数及片厚有关的系数；f、Bm、V与前面介绍的相同。铁心总损耗：

$$\Delta P=\Delta P_{Cu}+\Delta P_{Fe}=\Delta P_{Cu}+\Delta P_{h}+\Delta P_{e}$$

铁心的损耗，工程上往往用实验方法测出，而用公式计算会很麻烦。

练一练

将一铁心线圈接在电压220V、50Hz的电源上，其电路I1为2A，功率P1为132W。将此线圈接在6V直流电压上，其电流I2为2.18A。问此线圈工作在220V、50Hz时的铜损和铁损。

解：铜损：线圈电阻r=6/2.18=2.75Ω

$$\Delta P_{Cu}=I^{2}_{1}r=2^{2}\times 2.75=11W$$

铁损：铁损等于总损耗减去铜损：

$$\Delta P_{Fe}=132-11=121W$$